ES común en los libros de bachillerato incluir una introducción a la mecánica cuántica dentro de su sección de física moderna. Cómo sé que mucha gente esta ahora a punto de empezar a preparar la selectividad y les entra en el temario, voy a hacer una presentación del tema. Conociendo los libros y cómo tratan la materia voy a intentar que el post complemente en parte esos libros, aunque, no por ello, deja de ser este post una presentacion autocontenida. Empiezo por presentar algunos conceptos matemáticos necesarios para un correcto entendimiento de la cuántica. Manejar bien esos conceptos, tener soltura con los cálculos, requiere una formación extensa, pero los conceptos en sí no son muy dificiles de entender.
Concepto de ecuación diferencial:
Los planes de enseñanza contemplan que todo el mundo sepa que es una ecuación algebraica.
Esto es una expresión que puede ser algo tan sencillo como lo siguiente:
2x + 1 = 0.
Todo el mundo sabe resolver esto. 2x= -1 => x= -1/2.
Bien, en física muchas de las leyes no se expresan por ecuaciones (o expresiones) algebraicas. Lo normal es que se expresen por ecuaciones difererenciales.
La mas famosa de ellas es la segunda ley de Newton F=m.a. En la fisica de bachillerato se empieza explicando cinemática y se habla del movimiento uniformemente acelerado, con lo cuál a es constante. Si a priori sabemos que el ejercicio va describir un movimiento unifromemente acelerado la segunda ley de Newton puede tratarse cóm una ecuación algebraica, pero ese planteamiento puede llevar a ocultar un poco su verdadera naturaleza como ecuacion diferencial. La forma correcta de expresar esta ley es:
(S(t) es la posicion de la partícula en el instante t)
F en general dependerá a su vez de S, y posiblemente de t. Si el problema es en una dimensión podemos usar la coordenada x en lugar de S.
Cojamos un caso típico, el oscilador armónico. aquí F= k.x. (k es la costante recuperadora del muelle y es normalmente algo que se conoce, no una incógnita). Así la ecuación queda :
Quiere esto indicar que x indica la posición de la partícula y esta partícula se va desplazando en el tiempo.
Si pasamos el lado derecho de la expresion anterior restando al lado izquierdo resulta:
.
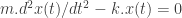Esto se parece bastante a las ecuaciones algebraicas del principio. La diferencia es que allí x representaba un valor que debíamos determinar. Aqui representa una funcion de t que debemos determinar. Otra diferencia básica es que allí x aparecía multiplicada por números, aquí ademas aparece derivada.
Voy a recalcar el , muy relevante, hecho de que la función a determinar, x(t), o sus derivadas, no aparecen elevadas al cuadrado o potencias superiores. Es una ecuación diferencial lineal. Aunque en físia hay ecuaciones diferenciales no lineales (por ejemplo en dinámica de fluidos) hay mucha física que se puede describir mediante ecuaciones lineales. Tampoco he mencionado otro hecho que no viene mal conocer. El orden de una ecuación diferencial hace referencia a la máxima derivada que aparece. Aquí la función como máximo aparece derivada dos veces. Por tanto es una ecuación lineal de segundo orden.
Es más, como no hay nada que dependa de la variable independiente, t, si agrupo las expresiones que incluyen la función incógnita y/o sus derviadas ya la izquierda el resto de expresiones resulta que a la derecha no hay nada. Es una ecuación diferencial lineal de segundo orden homogénea. No haré mas hincapien en la clasificación de las ecuaciones diferenciales, de momento.
¿Como se resuelven ecuaciones diferenciales? En la universidad hay asignaturas anuales para enseñarte a resolver una serie de ecuaciones diferenciales lineales básicas. Aquí me limitaré a exponer como resolver esta.
Para ello recordar que si x(t) = sen w.t su derivada es x'(t)= w. cos w.t
Y que la derivada de x(t) = cos w.t es , introduciendo otra notación también habitual y conocida, (cos wt)’ = -w.sen wt.
Esto es muy interesante, implica que (sen w.t)»= -w2 sen wt.
Es decir, la derivada segunda de la función seno es ella misma, multiplicada por un factor. Mirando atentamente nuestra ecuación uno se da cuenta de que una función seno esla candidata ideal para ser nuestra solución. Nos faltaría saber cuál es w.
Si aplicamos lo visto nuestra ecuación queda:
-w2.m.sen(wt) – k sen(wt) =0
Sacando factor común queda: [-w2.m – k].sen(wt)=0
Pero sen(wt) en general no es 0 para un valor arbitrario de t. La única posibilidad es que lo que lo multiplica sea 0.
Es decir -w2.m – k=0
Esto es una ecuación algebraica para w. Sabemos resolverla. w= (k/m)1/2. En realidad podríamos pensar que el mismo valor con un signo menos valdría.
Incidentalmente resulta que esta w es la frecuencia de oscilación del muelle. Con lo cuál recuperamos la información que se suele obtener en la física de secundaria. De hecho esta observación sirve para descartar la otra posibilidad que se nos presentaba, haber elegido la solución para w con valor negativo.
He calculado una solución. En realidad hay dos soluciones linealmente independientes. Y cualquier combinación lineal de ellas es solución. En el oscilador armónico la otra solución sería cos wt, dónde w tendría le mismo valor de antes.
En general una ecuación diferencial admite muchas soluciones. Pero si se complementa la ecuación con información adicional, en el ejemplo aquí tratado sería la posición y la velocidad del extremo del muelle en un instante dado, la solució que cumpla esas condiciones adicionales es única.
Concepto de derivada parcial:
Recordemos que es una derivada parcial. El concepto surge cuando se tiene una función de varias variables, por ejemplo:
f(x,y,z)= sin x + x.y.z2.
Por ejemplo f podría representar la temperatura del gas en una habitación. Cada punto de la habitación correspondería a un valor concreto de las variables x,y,z y tendría una temperatura indicada por el valor de f en ese punto.
Entonces la idea es que se puede tomar la derivada con respecto a cada una de las variables y que el resto se traten como constantes.
Así por ejemplo quedaría:
∂f(x,y,z)/∂x= cos x + y.z2.
Nótese que aquí la derivación se indica con ∂/∂x en lugar de con d/dx. Normalmente se sigue usando esta notación hasta cuarto de carrera. Una vez allí, que la gente ya se ha familiarizado, se cambia por una notación abreviada, que es la que usaré en adelante. Se substituye ∂/∂x por ∂x. Evidentemente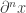 
significa la derivada enésima respecto a x. (derivar n veces respecto a x).
Por supuesto se pueden hacer derivadas cruzadas, por ejemplo:
∂xy f = z2.
Se puede demostrar que si f cumple condiciones razonables se cumple que ∂xy=∂yx (derivar primero con respecto a x y luego respecto a y es lo mismo que hacerlo en el orden inverso)
Ecuaciones en derivadas parciales:
Una vez explicado que es una derivada parcial es sencillo entender que es una ecuación en derivadas parciales. Una identidad en la que se igualan diversas derivas parciales de una función de varias vaariables que será nuestra incógnita. Por ejemplo:
∂xx f(x,y) + ∂yy f(x,y) =0
Es decir debemos encontrar una función de dos variables cuya derivada segunda respecto a x sumada a su derivada segunda respecto a y sea igual a 0. Normalmente no se indica el número de variables de los que depende f, pues suele poderse averiguar fácilmente por la misma forma de la ecuación.
Antes de pasar a las técnicas de solución debemos detenernos en un aspecto importante. Las condiciones iniciales.
En una ecuación diferencial ordinaria, en que la funcion sólo depende de una variable, vimos antes que hay varias soluciones posibles a la ecuación, pero si especificamos el valor de la función, y el de su derviada, para una x0 dada, es decir f(x0)=C0, f'(x0)= C2,
En el caso de las ecuaciones de movimiento debíamos fijar la posición y la velocidad en un instante dado de tiempo para fijar una solución única. Esto es el llamado teorema de existencia y unicidad. Esta probado para ecuaciones tanto lineales como no lineales.
Las ecuaciones en derivadas parciales (a partir de ahora EDP’s) son mas complicadas, se clasifican en parabólicas, hiperbólicas y elípticas. Cada tipo requiere un tipo especial de condiciones de frontera (que ya no iniciales).
No discutiré todos los casos. Sólo uno, muy importante para la mecánica cuántica. La ecuación de onda (que es de tipo hiperbólico), nos centraremos en el caso mas sencillo, la unidimensional:
1) ∂xxΨ -1/c2∂ttΨ=0
(denoto la función incógnita por Ψ, que es una notación standard para la función de onda en mecánica cuántica)
No analizaré la teoría general (no es muy necesario para nuestros propósitos). Analicémoslo desde un punto de vista intuitivo y físico.
Esta ecuación podría representar en mecánica clásica una cuerda vibrando. La cuerda estaría extendida en el eje de las x y las vibraciones podrían se en el eje de las y. En ese caso Ψ denotaría la amplitud de la vibración en la coordenada Y en el punto x de la cuerda.
¿Que condiciones sería normal imponer? Físicamente una situación común sería que la cuerda estuviera sujeta en ambos extremos, que serían x=0 y x=L (L= longitud de la cuerda). Esto matemáticamente se expresa por:
Ψ(0,t)=Ψ(L,t)=0 (para todo valor de t, normalmente eso se indica con una A invertida, pero no encuentro como representar ese símbolo en HTML)
Estas son condiciones en el extremo de la cuerda. En un caso mas general serían condiciones en el contorno de un recinto. Por eso en EDP’s es común hablar de condiciones de contorno.
¿Que mas podemos necesitar? No he explicado de dónde sale esta ecuación. Se puede deducir de las ecuaciones de Newton. Se parte de una situación con muchas partículas en el eje x y se hace el paso al límite en que en cada posición del eje hay una partícula. Es el paso al continuo, y lo que se llama mecánica de medios continuos.
Al venir de las leyes de Newton sabemos que necesitamos conocer la posición y la velocidad de cada punto de la cuerda en un instante, por ejemplo para t=0
Ψ(x,0)=f(x), ∂xΨ(x,0)=g(x), dónde f y g son dos funciones que podemos tomar arbitrariamente (salvo las restricciones habituales de que no sean demasiado patológicas, no entraré en detalles por ahora).
Bueno, esta es una selección posible de condiciones iniciales y de contorno para este problema. Hay mas posibilidades, pero esta es la mas sencilla.
Dije que esto estaba relacionado con la mecánica cuántica. En realidad el mismo problema matemático podría representar una partícula cuántica atrapada en un «pozo infinito», es decir, una región de la cuál una partícula cuántica no puede salir.
Hay algunas diferencias. Voy a exponer aquí algunos postulados de la mecánica cuántica, sin explicar mucho de dónde surgen y luego pasaré a analizar como resolver el problema matemático planteado.
Primer contacto con la mecánica cuántica
¿Que representa Ψ en mecánica cuántica?
La probabilidad de que la partícula este en la posición x.
Para una partícula cuántica no se puede determinar a la vez la posición y la velocidad con precisión absoluta.. Este es el famoso principio de incertidumbre de Heisenberg. Se cumple que:
2)ΔX.ΔP=h/2π
(ΔX es la indeterminación en la posición, ΔP es la indeterminación en el momento, el momento es el producto de la masa por la velocidad, h es la constante de planck)
Una consecuencia del principio de incertidumbre es que ya no se puede hablar de que una partícula siga una trayectoria. Toda la información sobre un sistema cuántico (la posición más probable, la velocidad mas probable, la energía, etc) la debemos obtener a partir de su función de onda, que lo describe completamente.
¿Como obtenemos esa información?
Mediante unos objetos matemáticos llamados operadores. la posición nos la dará el operador posición, la velocidad (o equivalentemente el momento) el operador momento, la energía el ¿operador energía?, no , el Hamiltoniano, ya veremos que es y de dónde surge.
Para poder avanzar vamos a ver que forma puede tomar una función de onda. Su nombre indica que debe cumplir una ecuación de onda.
Si sustituimos en la ecuación 1) veremos que Ψ(x,t)= sen (kx – ct) cumple la ecuación (sin ocuparnos de las condiciones de contorno). La ausencia de condiciones de contorno significa que la onda/partícula puede ir a cualquier lado.
Esto representa en el caso clásico una ondulación de la cuerda avanzando en la dirección positiva del eje x a una velocidad c.
Se podría usar esta función, no obstante es mas común usar la exponencial compleja.
3) Ψ(x,t)= exp {i(kx – wt)}=cos(kx -wt) + i.sen(kx -wt)
La última igualdad proviene de de la forma polar de escribir un número complejo. Asumiré que el lector esta familiarizado con los números complejos.
¿Por qué trabajar con funciones de onda compleja?. En realidad no es imprescindible. Pero facilita mucho el formalismo. Así que normalmente en los cursos de mecánica cuántica se postula que estamos en un espacio de Hilbert complejo de las funciones L2 de cuadrado integrable y no se dan demasiadas explicaciones.
Al fin y al cabo ya se supone al estudiante familiarizado con espacios de Hilbert. De momento no he dicho que es un espacio de Hilbert. Ya veremos su origen cuando resolvamos la ecuación de ondas, mas adelante. Pero por el momento no necesitamos saber que es.
Hasta ahora he saltado a hablar de función de onda sin dar muchas explicaciones de porque se hace esto. Después de todo en mecánica clásica describíamos una partícula por la evolución su posición en el tiempo, su trayectoria.
Ya se dijo al hablar del principio de incertidumbre que eso no es posible. Pero el motivo histórico por el que se introdujo la función de onda es otro. Proviene de una vieja discusión sobre la luz. La luz ¿es una onda o es una partícula?
Newton afirmaba que era una partícula. Que la luz que veíamos estaba hecha de muchas partículas.
Sin embargo por esa misma época huygens hizo una serie de experimentos que indicaban que la luz tenía un comportamiento ondulatorio. En el siglo XIX James Clark Maxwel resumió todo lo que se había averiguado hasta ese momento sobre electromagnetismo en cuatro ecuaciones.
De esas cuatro ecuaciones podía deducirse que en ausencia de cargas también podía haber campo electromagnético. Ese campo electromagnético seguía una ecuación de ondas (vectorial). Las ondas de una cierta frecuencia eran la luz visible. Otras longitudes de onda se usan hoy para la radio, los teléfonos móviles. También aparecen de manera natural en elementos radiactivos, los rayos x, los rayos gamma, etc.
Eso parecía zanjar la cuestión. Sin embargo unos experimentos muy a finales del XIX y a principios del siglo XX volvieron a sembrar la duda. En concreto el efecto fotoeléctrico y el efecto compton.
El efecto fotoeléctrico es una discrepancia entre la energía que adquieren los electrones que escapan de una lámina de metal bajo la iluminación de ondas electromagnéticas.
Según la teoría clásica la energía que adquirían estos electrones dependía de la intensidad de la luz. Pero en realidad se observaba que no era así. Su energía dependía de la longitud de la onda.
Einstein interpretó esto introduciendo el concepto de fotón. Decía que la luz estaba formada por corpúsculos. Para explicar el efecto Einstein asignó a estos corpúsculos, que denominó fotones, una energía:
4) E = hv (dónde v es la frecuencia de la radiación y h, de nuevo, la constante de planck)
Por esta explicación es por la que Einstein recibió el premio nobel de física, y no por la teoría de la relatividad, como usualmente se cree.
El efecto compton consiste en que si la longitud de los fotones incidentes es aún mas alta pueden chocar con los electrones y cambiar su frecuencia.
Esto se explica asignado al fotón no sólo energía sino cantidad de movimiento, o momento, en concreto:
5) p= hv/c
Así que los fotones tienen un claro comportamiento como partículas. Pero según Maxwell también quedan bien descritas muchas de sus propiedades mediante una ecuación de ondas.
Mas adelante otros experimentos demostraron que en ciertas circunstancias los electrones, que claramente parecían partículas, podían comportarse como ondas. Se les asigno una longitud de onda, la longitud de onda de deBroglie:
6) λ =h/p
Y de ahí se llegó a describir las partículas mediante una función de onda que indica la probabilidad de hallar la partícula en un punto.
Hemos hecho un largo desvío en nuestro propósito de ver como obtener información de la función de onda. No ha sido en vano, ahora veremos por qué.
Recordemos la ecuación 3. Esta describe una partícula desplazándose libremente con velocidad v=k/m (m la masa de la partícula) y frecuencia w. Si la partícula no se desplazar libremente la ecuación que regiría su movimiento sería diferente.
Normalmente habría un término que indicaría que esta sometida a un potencial. O también se puede caracterizar cierto tipo de potenciale por condiciones de contorno. Por ejemplo el «pozo infinito» es un potencial cuyo valor es muy alto, idealmente infinito, en todo el espacio, excepto en una región determinada. De momento vamos a seguir trabajando con la partícula libre.
Hemos de suponer que representa una partícula con momento k. ¿que operador sería adecuado para esto?
Bien, sería:
P x= -ih/2m . ∂x
Es decir, el operador momento (para ser exacto su componente x) consiste en derivar la función de onda respecto a x y multiplicar el resultado por -ih/2m.
Se puede verificar que si hacemos eso sobre la función de onda 3 obtenemos que:
P x Ψ= k. Ψ
Es decir que el resultado de actuar con el operador momento sobre la función de onda es equivalente a multiplicar esta por k. Normalmente en mecánica cuántica un operador se indica poniendo un ^ sobre la letra. Sin embargo por simplicidad de escritura me limito a denotar los operadores poniéndolos en negrita (cuando necesito distingirlos de su contrapaartida clásica porque no quede claro por el contexto cuando hablo de unos u otros).
Esto se cumple sólo para funciones de onda de una forma particular. Las funciones que cumplen esto se denominan autofunciones del operador momento. Son las que tiene un momento bien definido.
Si elogiáramos al azar una forma para la función de onda, por poner un ejemplo 1/x2 + 1 veríamos que el resultado de actuar sobre ella el operador momento nos daría una nueva función que no es equivalente a multiplicar la función original por un número.
Esto significa que no tienen un valor definido del momento.
Para que quede mas claro. Si sabemos que un estado cuántico va a estar descrito por una función de onda que es autofunción del operador momento eso significará que si hacemos un experimento para medir este momento nos dará siempre el mismo
Sin embargo si disponemos un sistema cuántico en una situación que se describe por una función que no es autofunción del momento y medimos experimentalmente este momento obtendremos que unas veces se observa que unas veces tiene un momento y otras algún otro omento distinto (los valores obtenidos dependería de la función que hubiéramos elegido).
Si repetimos muchas veces esos experimentos incluso veríamos que a cada uno de los momentos posibles le corresponde una probabilidad de que al hacer la medida se obtenga ese valor. Por todo esto decimos que esa función, que no es autofunción, no tiene un valor bien definido del momento.
Vale, ya tenemos el operador momento. ¿que hay del operador que nos da la posición de la partícula?
Recordemos que interpretamos la función de onda como indicadora de la probabilidad de hallar una partícula en un punto.
Una propiedad de la ecuación de ondas es que se trata de u na ecuación lineal. Esto implica que si Ψ es solución y φ es solución su suma también es solución (ejercicio, demostrarlo).
Recuerdese que en cierto sentido la integral es una suma. Así podemos hacer una «suma» de un infinito continuo de soluciones de la ecuación de onda libre. Cada solución viene indicada por un valor de k. Como estamos trabajando en un instante de tiempo fijado nos desentendemos de la parte temporal de la función de ondas.
Consideremos en concreto:
7) Ψ(x,0)=1/2π .∫dk f(k).eikr
Dónde 
Esto es un «paquete gaussiano».
Va a representar un paquete de ondas centrado en cero y con una anchura |x|< a
¿Como sabemos esto? Habíamos dicho que la función de onda representaba la probabilidad de hallar la partícula en un punto x. Pero no habíamos dado una expresión matemática. Esta representación matemática es:
Probabilidad de hallar la partícula (para t=0) en x=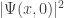 
.
Aplicada al paquete de ondas 7 nos daría:
.
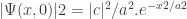que es una función gausiana centrada en 0 de anchura a. de los cursos de probabilidad sabemos de sobra la forma de esta función. Si no es el caso puede representarse gráficamente y comprobarse que su dibujo claramente indica lo que afirmamos.
La interpretación probabilística de la mecánica cuántica nos dice no sólo que la función de onda hace lo que ya hemos dicho. También afirma que el valor medio de un operador debe obtenerse considerando la función de onda como distribución de probabilidad.
Es decir, que el valor medio de un operador op es ∫dx Ψ*opΨ.
Queremos que el operador posición (su componente x) X de sobre ese paquete de ondas un valor medio 0. Es sencillo comprobar que si ponemos:
XΨ= x.Ψ
(Es decir el operador x actúa sobre la función Ψ multiplicándola por x) obtenemos lo deseado.
Ya sólo nos faltaría hablar del operador hamiltoniano. Este operador representará la energía del sistema. Podies leer detalles sobre el hamiltoniano, y el lagrangiano, en los posts anteriores. Si no os apetece simplemente señarlar que en lo scasos sencillos el hamiltoniano clásico es la energia del sistema, y en muchas ocasiones tendrá la forma sencilla H= T + V. Aquí T es la energía cinética 
, que usando la conocida expresion para le momento p=m.v puede ponerse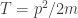 
y V es la energía potencial. Pués bien, la idea es escribir el hamiltoniano clásico y sustituir el momento clásico por el operador momento y la posición clásica por el operador posición. Eso nos lleva a la ecuacion de Schröedinger dependiente del tiempo:
Sin embargo en muchas de sus aplicaciones basta con ocuparnos de estados estacionarios, que no evolucionan en el tiempo más que cambiando su fase de manera trivial (multiplicando por una exponencial). Esos estados cumplen la ec. de Schröedinger dependiente del tiempo:
Para un caso típico la forma explicita de la ecuación, una vez sustituido en el hamiltoniano la expresion de los operadores sería:
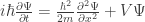
Aahora tocaría ver como se obtiene la solución general de una ecuación en derivadas parciales. Eso nos permitirá entender mejor de dónde sale el considerar que la funcion de onda pertenece a un espacio de hilbert, y entender de dónde saldrán algunos postulados mas de la mecánica cuántica. Pero creo que, con todo, hayan quedado claros aalgunos conceptos básicos de la mecáncia cuántica .
.
con 
se tiene que 
tiene signo opuesto a 
. Esto significa que este observador ve una inversión del intervalo temporal. Para él, el taquión no ha ido del punto x1 al x2, sino al revés. Esto ya da una idea de que cuando hay taquiones de por medio la ordenacion temporal de acontecimientos puede invertirse, pero aún sigue sin ser claro cómo esto permite enviar mensajes al pasado. Enseguida voy a ello, pero antes un breve inciso para señalar otro aspecto interesante relacionado con esta misma circunstancia, la dependencia del signo de la energía del taquión en el observador. La ley de tranformación de la energía es:
(aquí se ha hecho c=1)
Estos eventos sucederán en tiempos 
y 
para el observador 2.
puede verificarse facilmente que no hay ninguna anomalía en las ordenaciones temporales. Sin embargo si no se cumple (tomándose, por ejemplo que las velocidades de los taquiones son ambas infinitas) puede verificarse que se llega a que:
Ciencia DiY 