Pedro y el (lo)bosón a 5.1 sigmas

Como dije en una de las últimas entradas este blog había entrado en hibernación hasta que no hubiera algo que realmente tuviera buenas expectativas de ser nueva física.

Hace poco estuve a punto de escribir sobre el hecho de que un nuevo experimento había vuelto a encontrar evidencia de la anomalía del momento magnético del muón, lo cual requeriría física mas allá del modelo Standard. Es un resultado sólido y prometedor, pero no está aún madura para que haya perspectivas de un anuncio inminente y definitivo al respecto, así que lo dejé estar.

Tampoco hablé de la triste muerte de el mas grande de los físicos que crearon el modelo standard, Steven Weinberg, y que nos ha dejado con únicamente Gerard t’hooft como representante de lo mejor de esa generación, que es la última que, estrictamente, son físicos teóricos de éxito contrastado. Y estamos hablando de gente que hizo sus mejores trabajos hace acreedor de 50 años.

El caso es que hoy he visto en el blog de Lobos (https://motls.blogspot.com/2021/09/an-informal-atlas-cms-combo-new-1515gev.html) y sólo ahí, el anuncio de un nuevo bosón escalar a una evidencia local de, ni más ni menos que 5.1 sigmas. La evidencia global, eliminando el efecto «look somewhere else» se reduce un poco mas, y se queda en 4.8 sigmas. Eso estrictamente no son los 5 del descubrimiento «oficial», pero es prácticamente imposible estadísticamente que, sí se ha llegado hasta allí, no se sigan encontrando mas señales según se analicen mas datos, así que debería ser un descubrimiento.

El artículo original de arXiv es Accumulating Evidence for the Associate Production of a Neutral Scalar with Mass around 151 GeV. Es un artículo corto, 7 páginas, y totalmente «cacharrológico». Es decir, no hay discusión de los aspectos teóricos y los modelos que se están analizando sino como se analiza si hay o no evidencia experimental de los mismos. El contexto general de esos modelos surge del MSSM (minimal supersymmetric standard model) que es la extensión supersimétrica mas sencilla posible del modelo standard. Ese modelo hace mucho que está desechado experimentalmente, pero es la base de muchos otros modelos que son variantes suyas, y algunos de ellos no están descartados.

En el MSSM el bosón de Higgs del modelo standard no estaría sólo. Por supuesto tendría su compañero supersimétrico, un Higgsinos, pero eso no es todo el asunto.

Como se puede observar en la figura el MSSM predice la existencia de cinco bosonoes de Higgs. Uno de ellos seria el ya descubierto, que sería el mas ligero. También habría dos bosones cargados, H+ y H- y dos Higgs neutrales extra, A/H. Se pueden encontrar mas detalles al respecto en, por ejemplo Why should there be only one? Searching for additional Higgs Bosons beyond the Standard Model

Los autores del artículo (que no es un artículo oficial del CERN, pero sí es un artículo hecho por profesionales plenamente contrastados expertos en ese campo) habla de algo llamado 2HDM+S, que desconozco totalmente, pero se deduce que debe ser una variante del sector Higgs extendido del MSSM. En concreto lo que les interesa es que habría un bosón neutral escalar H, que decaería en otro bosón S y en el higgs del modelo standard. Los bosones de higgs son letones, es decir, no interactúan con la energía nuclear fuerte así que ese evento de decaimiento es un caso particular de un proceso dileptónico.

El caso es que combinando diversas observaciones separadas en una sola logran obtener esa abrumadora evidencia estadística, que, prácticamente, es un descubrimiento. Aparte del decaimiento estudiado ese bosón original H puede decaer a otros tipos de partículas, y han hecho una búsqueda dentro del los datos del LHC sobre si existen o no evidencias de algunos de esos otros posibles procesos. De algunos de ellos encuentran alguna evidencia, y de otro dicen que aún no. En caso de que no se encontrara el evento faltante habría otros posibles modelos que serían compatibles.

Recapitulando: Tenemos una gran evidencia estadística, que es casi imposible que sea una fluctuación. Se podría explicar por física que está dentro del marco de la supersimetría, que sería el siguiente peldaño después del modelo standard, según las ideas teóricas sobre las que hay mas consenso. Y parece imposible que esa evidencia estadística tenga origen en algún error sistemático. Lubos menciona una aportación, que no está en el artículo sobre que la masa de ese bosón escalar estaría cerca de la de dos bosones vectoriales W, lo que, quizás, aunque es muy poco probable, podría indicar que haya alguna mala interpretación de algunos datos. Además, antes de este artículo ha habido bastantes otros que apuntaban a algo similar, aunque con mucha menos contundencia.

Total, que aunque no tiene aún el rango de una evidencia firme e incontrovertible no está muy lejos de serlo. Y, lo que es mejor aún, no parece que pudiera ser muy difícil hacer análisis complementarios de lo que ahí se estudia y que puedan corroborar (lo mas probable, aunque quizás se llegase a rebatir) y que estén listos en poco tiempo.

Es decir estaríamos a los prolegómenos de la salida de la física teórica de un periodo de crisis en cuanto a nuevos resultados experimentales que ha durado alrededor de 50 años. Los autores del artículo se llevarían el Nobel ipso facto y los libros de supersimetría se tendrían que reescribir para analizar, aparte de las bases, los modelos que tienen este proceso. No conozco el 2HDM +S, pero estoy seguro de que, aparte de este proceso, hará mas predicciones y tal vez algunas de ellas, ya sabiendo a tiro hecho lo que hay que buscar, puedan traer nuevos descubrimientos del LHC.

Por supuesto, una vez verificada la supersimetría, la teoría de cuerdas habría ganado un respaldo experimental que, aún siendo aún estrictamente indirecto, ya sí que sería muy difícil de discutir.

Lo que mas me llama la atención es que un artículo como este, que es el que mejor pinta tiene en la historia del LHC, sólo haya aparecido en el blog de Lubos, y que nadie haya comentado nada al respecto. En los primeros tiempos del LHC ahora mismo estaría en casi todos los blogs del mundillo, y habría montones de discusiones al respecto yendo y viniendo. Realmente no sé porqué no es así. Tal vez se esté hablando de ello en phsyic stock exchange, pero no me gusta demasiado el formato de esa página, y no la sigo. Tal vez sea, como apunta el título de la entrada, que ha habido tantos «que viene el lobo» (va a haber un descubrimiento importante) que, cuando realmente llega ya nadie presta atención.

Sea como sea me parecía que no podía dejar de lado esa noticia y por eso he escrito este artículo cuando, realmente, debería estar ocupado en otros menesteres, pero no quería contribuir al atronador silencio con que ha sido recibido el artículo.

Divertimento sobre los viajes en el tiempo

Ahora que estamos en medio de una para nada inesperada pandemia mundial (con el volumen de turismo mundial, y todos los avisos anteriores era cuestión de tiempo, recobro una entrada que puse en facebook en Diciembre del año pasado, con intención de, tal vez, desarrollarla un poco formalmentey presentarla al premio de la Gravity Research foundation, pero al final lo dejé así.

Posiblemente ahora alguien esté pensando en construir una máquina del tiempo y hacer una visita a Wuhan para evitar que alguien se coma una sopa de murciélago y tal vez lo pueda desarrollar por si mismo 😉

Sobre los viajes en el tiempo, una sugerencia para verlos desde otra manera muy reveladora.

Imaginad una civilización muy lejana, a muchos milenios luz de la tierra, y con algún telescopio idealmente perfecto, que pudiera ver todo lo que le llega, no importa cuan lejos esté, y que graba todo lo que recibe.

Entonces, si en un momento dado ve que alguien o algo desaparece, y, mirando con detalle, sospecha que ha podido viajar al pasado, revisa el vídeo y ve en que momento del pasado esa persona ha llegado a destino, y desde ahí lo que ha hecho, incluyendo cuando ha vuelto al futuro.

Desde la perspectiva de esa especie no habría violaciones de causalidad, al menos global, porqué tendría una visión global de todo lo que ha pasado.

Otro punto interesante es el tema de la masa. Sí alguien/algo viaja al pasado la masa del universo en ese tiempo habría disminuido, y en el destino habría aumentado.Por contra, en el destino, la masa habría aumentado.

¿Cómo se podría compensar éso? Bueno, los taquiones, que pueden viajar mas rápido que la luz y generar paradojas temporarles, tienen masa imaginaria, pero su acoplamiento, a nivel cuántico,con la relatividad general se hace mediante la ecuación de Klein-Gordon en espacios curvos y el tensor de energía-momento que se deriva de ella. En esa ecuación, y en el tensor energía-momento, la masa aparece al cuadrado. y es por tanto negativa.

En función de éso, si cada vez que hay un viaje al pasado, se emitieran taquiones hacia el pasado en cantidad exacta para compensar la que viaja en el tiempo, en el futuro la variación de masa sería 0 (se ha perdido masa negativa, que es como ganar masa positiva, que compensa la que ha ido al pasado con el viajero del tiempo).

Pero si, además, esos taquiones que vienen del futuro en ese pasado habrá una cantidad de masa negativa extra que compensará la que ha añadido el viajero del tiempo.

Cuando el viajero del tiempo regrese el proceso sería a la inversa.

Mas interesante aún es que esos taquiones viajan mas rápido que la velocidad de la luz, así que pueden usarse para enviar información a través del tiempo. Eso, obviamente, abre la posibilidad clara de que, de algún modo, esos taquiones que tan oportunos son para permitir la conservación de masa, además, puedan llevar información entre los puntos dónde se ha producido el salto temporal que sirva para contrarrestar cualquier paradoja, aunque aún no me he puesto con los detalles de como podría ser éso.

Los taquiones, en principio, podrían interaccionar con la materia ordinaria, pero como no se han observado en condiciones normales esa interacción debe ser muy pequeña, pero ¿Y en condiciones no ordinarias?

Vamos a un agujero negro. De ahí no puede salir nada que vaya a la velocidad de la luz, o mas lento, pero un taquión si podría.

Cuando la materia ordinaria cae en un agujero negro va, según la relatividad general clásica, de manera inevitable hacia el centro, adonde llega en muy poco tiempo (propio).

El centro presenta una singularidad (una de las componentes de la métrica tiene un valor infinito que no se debe a una mala elección de coordenadas, como la del horizonte de sucesos).

Para la materia que cae ese es el punto final de su evolución temporal. Ahora bien, si esa materia normal tiene un acoplamiento a materia taquionica eso significa que, antes de llegar al centro, se podría convertir en taquiones (de nanera análoga a cuando un electrón y un positrón se convierten en un fotón). Normalmente no sería una reacción favorable, pero podemos asumir que, tal vez, cerca de la singularidad se vuelve cada vez más probable.

Una vez «taquionizada» la materia podría seguir moviéndose dentro del agujero negro, sin llegar a caer en la singularidad, pudiendo también ir «hacia fuera». Según se fuera acercando al horizonte de sucesos, desde dentro, la probabilidad de que el taquión se reconvirtiera en material normal aumentaría y, en ese caso, sólo unos pocos volverían a salir, y una vez fuera, volverían a ser mayoritariamente materia normal, y formarían la radiacción Hawking.

Para ver formalmente si ésto tiene sentido una de las primeras cosas sería saber cuál es la geodésica de un taquión. En relatividad general tenemos en los libros dos tipos de geodésicas, la convencional de geometría diferencial, que siguen las partículas de masa positiva, y las geodésicas nulas, que siguen las partíclas sin masa, como los fotones. He buscado un poco en google si había geodésicas de taquiones y no he visto nada, pero tal vez no he buscado lo suficente.

Luego está el tema de cuales serían las geodésicas dentro de un agujero negro, que también tienen su propia miga. Formalmente dentro de un agujero negro el radio se convierte en una coordenada de tipo tiempo y el tiempo una coordenada de tipo espacio. De todas formas lo mejor es ver este artículo de Fernando Lobo, autor bastante conocido en el ámbito de la relatividad general, sobre las geodésicas dentro de Schwarschild.

Interior of a Schwarzschild black hole revisited

Por cierto, si hablamos de taquiones dentro de un agujero negro también surgen curiosidades. En mecánica puramente clásica el taquión tiene masa imaginaria (aunque en la ecuación de K-G aparezca al cuadrado y tenga masa positiva).

Entonces ¿Que pasa con la solución de Schwarcshild para un taquión?

Si consideramos masa negativa tendríamos:

¿Que sentido tiene una métrica con un componente complejo? Bien, lo primero que habría que hacer es descomponerla en su parte real, que nos debería dar la parte «ordinaria» y ver que pinta, osea, propiedades, tiene, y luego intentar lidiar con la parte compleja g= gr + i*gc. Para ello habría que reescribir el término temporal, que va elevado a -1. Haciendo éso quedaría primero:

La parte real sería, en la parte temporal la angular, el espacio-tiempo plano de Minkowsky en coordenadas espaciales. La parte real de la componente espacial ya no sería la de Minkowsky porqué estaría dividida por el denominador común de esa componente, .

¿Y la parte compeleja? En la parte temporal el término estaría dividido entre un factor así que sería muy pequeño. En la parte temporal aparecería el mismo término dividido entre el denominador común es decir:

En vez de seguir desarrollando expresiones, y como ésto es un divertimento y no un artículo serio de arxiv, intentemos pensar en significados físicos.

La idea de la métrica surge, en última instancia, de que la velocidad de la luz es invariante y que, para todo observador, se cumple que:

La métrica de Schwarschild modifica la de Minkowsky para reflejar la presencia de una masa. Si admitimos que hay taquiones la métrica de Schwarschild compleja modifica la de Minkowsky en presencia de un taquión, pero ¿Deberíamos ya partir de una métrica de Minkowsky con término complejo o sólo de una real? ¿Qué pintaría un término complejo en una métrica de Minkowsky?

De momento debemos darnos cuenta de que hemos introducido los taquiones, con masa compleja, simplemente para mantener real la expresión de la energía. Y, para empezar, hemos introducido los taquiones para tener partículas que puedan viajar mas rápido que la luz. Ahora bien, sí aceptamos que el espacio de partida de Minkowsky tiene una componente compleja deberíamos primero decidir que valor tiene la parte compleja, que debería ser fijo. Y luego encontrar que tipo de transformaciones dejan invariante esa métrica, las nuevas transformaciones de Lorentz. El caso es que quizás tendríamos que plantearnos que tal vez tendríamos unas coordenadas espaciales y temporales complejas en las que la masa compleja sería considerada masa real, y una velocidad en esas coordenadas complejas.

Se vuelve todo, como queda claro, demasiado «complejo». Pero, lo curioso es que no es una dificultad gratuita sino que surge de intentar incorporar masas negativas, que han surgido en relatividad espacial, a la relatividad general.

Sí usamos que los taquiones son partículas cuánticas descritas por la ec de K-G en el tensor energía momento, que da el acople de la métrica con la materia, la masa sería negativa y, en principio, podríamos pensar que tenemos un agujero blanco. Dejo aquí el tema, que nos desviamos del tema principal.

Por cierto, el botón de Higgs, antes de la ruptura de la simetría, era un campo de K-G taquiónico, y no me consta que ese aspecto haya recibido atención desde el punto de vista de la relatividad general (modelos cosmologicos), porque la inflación está relacionada con el término de potencial del inflatón (que podría ser el higgs o alguna otra partícula), pero no con el término de masa.

Venga va, otra historieta más sobre viajes en el tiempo.

Cuando se envía algo en el tiempo, sí lo que se envía tiene carga la carga total del tiempo de partida ha cambiado de manera brusca, y la del tiempo de destino también, pero en sentido contrario.

Lo curioso es que, para para cada partícula existe una antipartícula. Si las partículas no tienen carga ambas, partícula y antipartícula, son indistinguibles, pero si tienen algún tipo de carga las antipartículas tienen la carga opuesta.

Lo curioso es que, formalmente, las antipartículas viajan hacia atrás en el tiempo. De ese modo, si se envía una partícula con carga en el tiempo, por conservación de carga, se debería crear una antipartícula, que iría en dirección temporal opuesta, para conservar la carga, que justo es lo que hacen las antipartículas.

Esto, más lo que decía antes de los taquiones, es lo que me hace pensar que la relatividad ya lleva en su propia esencia elementos para lidiar con los viajes en el tiempo, que permite su estructura matemática, y, como expliqué en el post anterior, también con la paradoja de la información de los agujeros negros, usando taquiones, y sin recurrir de manera demasiado esencial a la mecánica cuántica, en particular sin requerir una teoría cuántica de la gravedad.

Por supuesto todo ésto que he explicado no pretender ser serio pero también es cierto es que parece encajar bastante bien.

Una última observación. La interpretación de los taquiones en la literatura no es consecuente de unos artículos a otros. Lo más «oficial» es la reinterpretación del campo taquiónico, que podéis leer en la wikipedia Tachyonic field, y anula bastante de la «literatura» qué he puesto aquí, pero tampoco es imposible que no se entienda del todo bien la relatividad especial (por no entender me refiero a que posiblemente haya una verdad mas profunda ahí escondida, y no precisamente algo que implique volver al éter sino mas bien al contrario, que haya algo aún mas sofisticado en algún lado detrás de la invariancia de la velocidad de la luz) y qué no esté todo dicho al respecto.

Cómo dije en el último post, no hay nada a nivel teórico que me llame terriblemente la atención, y por éso me da mucha pereza postear. No obstante sí hay una remota posibilidad de que algo realmente interesante ocurra en física de altas energías, y es que el presunto planeta X realmente exista, pero en forma de agujero negro. Se publicó un artículo sobre éso en Septiembre, que pasó bastante desaparecido para el grueso de la comunidad científica, pues no había visto continuaciones, aunque no para la prensa. Se puede leer al respecto en, por ejemplo:

Planet Nine may be a black hole the size of a baseball

Esta semana, sin embargo, ha habido una de, ni más ni menos que Edward Witten, posiblemente el físico mas famoso e importante después de la generación que creó el modelo standard. Dejo el enlace al artículo de Witten, que propone enviar 999 micronaves impulsadas por Laser a buscar ese microagujero negro.

Searching for a Black Hole in the Outer Solar System

El tema de ese agujero negro es realmente interesante, y he leído unos cuantos artículos para hacerme una idea de lo que podría representar, caso de existir. No prometo nada, ni mucho menos, pero lo mismo en algún momento publico algo sobre ello.

Resumen de descubrimientos importantes en física teórica acreditados experimentalmente desde la última entrada

Nada, no ha habido ninguno.

Avances formales con una pequeña probabilidad de llegar a ser relevantes algún día sí ha habido, pero no tengo claro que me apetezca demasiado emplear tiempo en hablar de ellos, ya se verá.

En cualquier caso el silencio en el blog se debe fundamentalmente a éso, que no pasa nada.

Sobre la génesis del modelo standard y sus sucesores.

Hay una frase famosa entre la generación hippy (allá por los 60/70) que rezaba aquello de «nunca confíes en nadie mayor de 30 años».

Por otro lado el premio mas famoso entre los matemáticos, la medalla fields, tiene el requisito de que el que lo reciba debe ser menor de 40 años aduciendo que nadie mayor de esa edad puede hacer una contribución importante e innovadora a las matemáticas. Éso es algo falso, cómo demuestra el contraejemplo, Joseph Fourier que creó su famosa teoría de series trigonométricas cuando estaba en la cincuentena (en una época en que la esperanza de vida, incluso corregido el sesgo de mortalidad infantil) no superaba los 30 años.

Entre los físicos hay otra frase «las teorías viejas no mueren, sólo lo hacen aquellos que las sustentan». Bien, todos sabemos que la física teórica actual no tiene grandes contribuciones experimentalmente probadas desde hace mucho, y que la gente mas famosa ya tiene «una edad». Pero, siendo gente experimental, vamos a ver los datos concretos, es decir, las fechas de nacimiento de las «grandes estrellas» de la física moderna. En el camino vamos a ver unas cuantas cosas que, al menos para mí, son un tanto sorprendentes.

1-La generación del modelo Standard de partículas, todos ellos premios nobel prestigiosos (última física fundamental verificada experimentalmente).

Murray Gell-Mann (padre del modelo de quarks, la base de la QCD. Para crear los quarks usó la teoría de grupos, que luego sería de importancia vital en física teórica): 1929

Setven Weinberg(El mas famoso, y mejor, de los físicos que crearon el modelo electrodébil): 1933
Sheldon Lee Glashow (co-descubridor del modelo electrodébil): 1932
Abdus Salam(co-descubridor del modelo electrodébil): 1926
Peter Higgs (el que introdujo el famoso bosón que lleva su nombre, y que sirve cómo medio para que las teorías gauge pudieran describir fuerzas en las uqe las partículas responsables de las mismas tuvieran masa): 1929
Gerardus ‘t Hooft (consagró el modelo standard al demostrar que las teorías gauge son renormalizables): 1946

Kenneth G. Wilson (autor de la teoría del grupo de renormalización, y la teoría de transiciones de fase, de importancia clave en teoria cuántica de campos): 1936

Excepto Hooft, y por muy poco, todos nacieron antes de la segunda guerra mundial ¡ahí es nada!

Y, dado que el modelo standard es una teoría gauge no abeliana, o teoría de Yang-Mills, debemos incluir a los inventores del concepto. Yang tiene el premio nobel, pero, de manera un poco extraña, Mills no.

Chen-Ning Yang: 1922
Robert Mills: 1927

Vamos con nombres ilustres del campo de la cosmología, que juega un papel fundamental en la física teórica actual, y, ya de paso, la relatividad general, base de la cosmología y los agujeros negros, otro ingrediente clave de esta física.

Stephen Hawking (probablemente el físico mas famoso del momento, así que no creo necesario detallar sus contribuciones): 1942

Roger Penrose(grandes aportaciones a la teoría matemática de la relatividad general, entre otras cosas, famoso también por haber escrito muchos libros de divulgación especulando sobre hipótesis que nunca ha llegado a probar, y que son poco verosímiles. En cualquier caso muy conocido y reconocido): 1931

Kip Thorne (otro de los grandes de la relatividad general, ganador del nobel de física de éste año por su contribución al hallazgo de las ondas gravitacionales por el experimento LIGO): 1940

Bien, seguramente me deje nombres importantes (en particular en QCD, que trataré mas adelante), pero creo que ésos son los mas relevantes de la física justo anterior a la teoría de cuerdas, la última verificada experimentalmente. El mas joven de ellos es Gerard t’hooft que tiene ahora la tierna edad de 71 años.

Vamos con los involucrados en la «prehistoria» de la teoría de cuerdas, en concreto con su prima cercana, la supersimetría. Sí consideramos cómo «padres de la supersimetría» a los autores del primer modelo famoso tendremos que hablar del modelo de Wess-Zumino.

Julius Wess: 1934
Bruno Zumino: 1923

Cómo se puede comprobar su edad está en el rango de la de los creadores del modelo standard. A diferencia del mismo la supersimetría no ha sido hallada experimentalmente. Realmente es algo relativamente inesperado pues hay muchas muy buenas razones para que ya se hubiera descubierto la supersimetría, y, en todo caso, la gente que la propuso pertenecía al mismo grupo generacional del modelo standard, que es una teoría de un éxito apabullante, y, realmente, el salto conceptual entre una y otra teoría es mínimo.

El siguiente paso después de la supersimetría es la supergravedad, es decir, supersimetría local, que da lugar a que, «mágicamente», aparezca por ahí la relatividad general. Sus padres son:

Daniel Z. Freedman: 1939
Sergio Ferrara (aparte de en supergravedad también hizo un trabajo pionero en teoría de campos conformes, un tema importante en física de materia condensada, pero sobre todo, en teoría de cuerdas ya que las teorías de cuerdas son teorías de campos conformes): 1945
Peter van Nieuwenhuizen (señalar que hizo la tesis con Martinius Veltman, el mismo que dirigió a Gerard `t hooft, y que compartió con éste el nobel por demostrar, en 1972, que las teorías gauge son renormalizables): 1938.

Una vez mas vemos que los autores de la supergravedad son, básicamente, de la misma generación que los autores del modelo standard. Es fácil tildar a los creadores del modelo standard cómo los «ganadores» y a los otros cómo «perdedores», pero, realmente, son gente que se formaron con la misma base, y que tenían métodos de trabajo muy similares. Para aclarar las cosas un poco mejor es necesario hilar mas fino con las fechas pertinentes.

En la síntesis del modelo electrodébil las primeras publicaciones de Sheldon Glasgow en el tema son de 1961, mismo año que las primeras de Salam. El trabajo clave de Weinberg es del 1966, tras el artículo de Higgs, de 1964. No conozco a fondo esa época y su cronología, pero sí he leído algunas cosas bastante aclaratorias sobre lo que había entonces.

La electrodinámcia cuántica de Feynman, Schwinger, Tomonaga y Dyson había sido un gran éxito y fué la primera teoría cuántica de campos renormalizable. Sus autores (excepto Dyson) recibieron el nobel en 1965, aunque sus trabajos clave son de entre 1947 y 1951 aproximadamente.

Posteriormente llegó la época de la física nuclear, o mas bien subnuclear. Al empezar los experimentos con aceleradores a las pocas partículas subatómicas conocidas (protón, neutrón, electrón, neutrino y mesones de yuakwa) se empezó a unir una pléyade de nuevas partículas, que en ese momento parecían fundamentales, aunque luego se vería que no, que no se sabía muy bien cómo encajar. Antes del modelo de Weinberg se tenía para la interacción nuclear débil el modelo de Pauli, que no era renormalizable, pero funcionaba muy bien. Para la interacción nuclear fuerte había muchos modelos bastante fenomenológicos, y lo mas parecido a una teoría fundamental eran los bosones de yukawa que mediaban la interacción nuclear entre protones y neutrones, que tampoco era renormalizable.

Poco a poco se fue creando algo de luz, con cosas cómo los partones, que son algo así cómo los precursores de la teoría de quarks. Pero la propia teoría de quarks es de 1964, es decir, dos años antes que la teoría de Weinberg. En cualquier caso la teoría de quarks (descrita por el SU(3) de sabor) es una teoría descriptiva, pero una teoría fundamental (éso sería la QCD, basada en el SU(3) de color, que vendría después, mas tarde comentaré cosas al respecto). En definitiva, que la única teoría renormalizable era la electrodinámica cuántica, y no había ninguna teoría renormalizable para la mayoría de interacciones. Aunque la generalización de la invarianza gauge de la electrodinámica, las teorías de yang-mills, ya se había hecho en 1954 no permitía incorporar partículas con masa. En se ambiente, según explica Weinberg, la mayoría de la gente no prestaba demasiada atención a las teorías gauge o a la propia electrodinámica cuántica cómo modelos de futuro y se centraba en el estudio de «las propiedades formales de la matriz de Scatering», usando mucha teoría de variable compleja, buscando polos (puntos dónde la función toma valores infinitos) en las amplitudes (asociadas a resonancias, que, a su vez, se asocian al descubrimiento de nuevas partículas). El caso es que era una época dónde primaban artículos muy formales en esa «matriz S» y trabajos con mas intuición física cómo los de Weinberg y los padres del modelo standard no eran para nada lo mas extendido y exitoso. De hecho Weinberg comentó que su artículo pasó prácticamente desapercibido por la gran mayoría de teóricos ¡3 años!. También comentó que escribió sobre teorías de yang-mills porqué la teoría de Matriz S le parecía un aburrimiento formal al que no podía aportar nada.

Volvamos al hilo. En 1966 estuvo el trabajo clave de Weinberg. El primer gran artículo sobre supersimetría es de 1973, 7 años mas tarde. Si creemos a Weinberg en que su trabajo tardó tres años en hacerse famoso éso nos da un intervalo de sólo 4 años de distancia entre ambos trabajos, uno un éxito rotundo a nivel experimental, y otro de relevancia empírica aún por demostrar.

Pero el caso es que el trabajo de supersimetría no es del todo posterior al modelo standard porqué tras el éxito de la teoría electrodébil con su grupo SU(2)xU(1) la gente estaba trabajando en la QCD y su grupo SU(3) de color.

La QCD describe los protones y neutrones (y el resto del zoo de partículas descubierto en esa época) cómo estados confinados de quarks. Sus dos aspectos mas rseñables son ese confinamiento y la libertad asintótica. En el confinamiento, un hecho experimental clave, surgido en la propia génesis del modelo de quarks, es decir, en 1964, la clave es deducir que la QCD presenta esa propiedad. Es un problema abierto, aunque hay un trabajo muy importante de Kennet Wilson (del que hablé antes) que usando lo que se conoce cómo «Wilson loops» da un argumento muy importante a favor de esa hipótesis. El trabajo dónde introdujo los wilson loops es de 1974, es decir, un año después de la primera teoría supersimétrica.

Antes de establecerse la QCD de manera firme se propuso otra alternativa para explicar el confinamiento, la teoría de cuerdas en quarks. El creador de esta teoría es Gabriele Veneziano (nacido en 1942) y su primer artículo en el tema es del año 1968, es decir, cuando el trabajo de Weinberg aún no era famoso, y anterior también al primer trabajo sobre supersimetría, luego, obviamente, esas no eran cuerdas supersimétricas, osea, supercuerdas, cómo las actuales). De hecho su teoría está inspirada en la «teoría de scatering de matriz S) y las amplitudes de Venciano. En esa versión muy primitiva (y diferente de la actual) de la teoría de cuerdas la idea era que los quarks estaban unidos por cuerdas. Estas, al estirarse, adquirían energía. De hecho sí se estiraban demasiado se rompían, pero antes habían adquirido tanta energía que en los nuevos extremos se formaba un nuevo par de quark y antiquark, lo cuál explicaba el confinamiento.

La otra gran pata de los aspectos elementales de la QCD es la libertad asintótica. éso significa que, a distancias muy cortas, la interacción entre los quarks se hace nula. Fue descubierta en en 1973 (el mismo año en que se introdujo la supersimetría) por David Gross (nacido en 1941, que, aparte de la libertad asintóntica, contribuyó al nacimiento y consolidación de la forma moderna de la teoría de cuerdas), y Frank Wilczek (nacido en 1951). Ambos autores ganarían el premio nobel por ese descubrimiento. Compartieron ese nobel con Hugh David Politzer (nacido en 1949) que ese mismo año publicó de manera independiente el mismo resultado.

Una tercera gran pata de la QCD sería su estructura de vacío, con cosas cómo los insatantones (1974 y 1977 primeros trabajos) o los monopolos de t’hooft y Polyakov (1974)
Cómo podemos ver, ahondando en las fechas, la supersimetría era una teoría que surgió a la estela de las bases del modelo standard (la teoría electrodébil, y la demostración de la renormalizabilidad de las teorías gauge un año antes) y compartiendo fechas con los años dónde la QCD tomaba forma (y los autores que le daban esa forma hacían méritos para el nóbel). Es curioso porqué, realmente, la supersimetría es una teoría mas «bonita» que todas las demás de la época y, por su relación primero con la supergravedad y luego con la teoría de cuerdas es, además, caso de ser cierta, mas fundamental e importante que el propio modelo standard.

La supergravedad nació en 1976, 3 años después de la supersimetría, y dos años después de la libertad asintótica, cuando aún se seguían cimentando muchos aspectos del modelo standard.

Ya, para cerrar, señalar otra teoría que daría forma a la génesis de la teoría de cuerdas, el modelo de gran unificación SU(5) de Giorgi (nacido en 1947) y el ya mencionado Sheldon Glasgow. Ése modelo es del año 1974, un año después de la supersimetría, y coetáneo ala libertad asintótica. Sus ingredientes son los mismos que los del muy exitoso modelo standard, una teoría de grupos gauge y, además, tiene un montón de aspectos sugerentes.

En definitiva, la física que triunfó (modelo standard) y la que «fracasó» (supersimetría, supergravedad, gran unificación, y su «hija», la teoría de cuerdas) fueron alumbradas prácticamente a la par, por físicos con similar bagaje y todas igualmente prometedoras. Sí acaso se puede indicar que la que tuvo éxito miraba al pasado, es decir, unía un montón de hechos experimentales previos en una única teoría SU(3)xSU(2)xU(1) mientras que las que «fracasaron» usaban las mismas ideas que estaban demostrando ser útiles para hacer previsiones sobre nuevos resultados futuros, siguiendo la costumbre de éxito del siglo XX en la que gente cómo Dirac había predicho el positrón, o Pauli el neutrino. De hecho el bosón de Higgs se predijo entonces y pasó mucho, mucho tiempo hasta que se descubrió (2012). Pero, lo importante, es que, mirando los detalles históricos no hay ningún motivo razonable para tachar a los que postularon las teorías «fracasadas» cómo algún tipo de soñadores que se salían de «el business as usual». Claramente estaban en el bussines a usual, y, de hecho, algunos de los que tuvieron éxito en parte también «fracasaron» (por ejemplo, no hay indicios experimentales de los solitones de t´hooft, que vendrían a ser, en algunos casos, instantones y en otros monopolos magnéticos). David Gross fué premio nobel por la libertad asintótica pero «fracasó» por su trabajo en teoría de cuerdas.

En cualquier caso ésa época, la génesis del modelo standard, coetánea con la de las teorías que deberían sobrepasarlo, es algo ya bastante «antiguo» y la gente que contribuyo a ello están o muertos, o con la edad de jubilación ya muy sobrepasada. Sí hacemos caso a la máxima del principio no deberíamos fiarnos de ellos, pero la cuestión es que fueron la última generación de teóricos que puede presumir haber obtenido resultados de éxito demostrado empíricamente.

Mi idea es, en algún momento, hablar sobre las diversas generaciones de físicos de cuerdas, desde los primeros a los mas recientes. Incluso yéndonos a la física de cuerdas los últimos nombres que realmente se puedan considerar cómo establecidos en el status de «famosos» ya no son precisamente unos chavales. Pero éso, dejo para un futuro esa historia, y tengo muchas otras cosas que contar, según vaya encontrando tiempo.

Ondas gravitacionales y nueva física

Se acaba de anunciar el descubrimiento de una cuarta onda gravitacional, esta vez observada por el nuevo detector Italiano, Virgo. Se puede leer sobre la noticia en muchos blogs, por ejemplo:

La onda gravitacional GW170814 ha sido detectada por triplicado (Francis)

LIGO and VIRGO Announce a Joint Observation of a Black Hole Merger (Matt Strassler)

Hace unos meses un grupo de investigadores sugirió que podría haber un error en el análisis de datos. Se puede leer un review sobre el tema por parte de Sabine Hossenfander aquí: Was It All Just Noise? Independent Analysis Casts Doubt On LIGO’s Detections, pero no parece que haya arrojado bastantes dudas sobre la validez de los descubrimientos previos, y ahora que un nuevo detector se ha unido a los descubrimientos, y ya con una cuarta onda, se le puede dar ya una gran credibilidad al hecho de que ya se han detectado ondas gravitacionales.

Además, tenemos que dentro de un tiempo se unirá al observatorio en tierra, LIGO, el observatorio en el espacio, LISA: Así es LISA, el proyecto europeo para entender el Universo.

Hasta ahora las ondas detectadas provienen de dos agujeros negros fusionándose en uno solo y se rumorea qué se han registrado datos de la fusión de dos estrellas de neutrones, aunque este fenómeno da una señal menos clara y su análisis requiere mas tiempo y por éso aún no ha sido reportado el conocimiento.

Todo ésto está muy bien, pero, ahora que ya podemos considerar razonablemente establecido el advenimiento de la época de la astronomía de ondas gravitacionales llega el momento de analizar que podríamos aprender de ello, y, la verdad, el potencial es amplio.

Ondas gravitacionales y agujeros negros

Dado que lo que se ha detectado hasta ahora son fusiones de agujeros negros el primer sitio dónde cabe esperar descubrir algo es sobre la física los mismos. Un análisis del tema lo tenemos en la entrada de Francis La formación de binarias de agujeros negros tras analizar las ondas gravitacionales de LIGO. Ahí analiza que hay tres hipótesis principales sobre cómo se pueden formar esos sistemas y mediante el espín proyectado de los agujeros negros incidentes se podría distinguir entre ellas, aunque para poder hacer éso hace falta descubrir aún mas fusiones. Para mas detalles leer el enlace.

Otro aspecto es que no se esperaba demasiado que hubiera agujeros negros de esa masa intermedia, mucho mayor que los que se forman por implosión de una estrella pero mucho menor que los que están en el núcleo de las galaxias. Éso es una incógnita para los modelos cosmológicos y reabre levemente la posibilidad de que la materia oscura, o al menos una parte de ella mayor de la esperada, se deba a agujeros negros. Sin duda ambos temas son interesantes en astrofísica y cosmología respectivamente, pero en física fundamental ya no tanto.

Cuerdas cósmicas y ondas gravitacionales

Las cuerdas cósmicas son un hipotético tipo de objeto astrofísico, consistente en filamentos muy largos, de muy alta densidad, formados cómo defectos topológicos en las transiciones de fase ocurridas durante la congelación del universo primordial. Explicar los detalles llevaría mucho tiempo así que dejo el enlace de la wikipedia al respecto para leer un poco más al respecto Cuerdas ¨Cósmicas. Ahí menciona que también puede haber cuerdas cósmicas de otro tipo, que vendrían a ser las cuerdas fundamentales de la teoría de supercuerdas, o también otro tipo de objetos de la teoría de supercuerdas. El tema de las cuerdas cósmicas es muy interesante y sin duda merecería una entrada aparte que ampliara lo poco que viene en la wikipedia,pero lo dejo para otro momento.

Las cuerdas cósmicas en un inicio se pensó que podrían tener un papel importante en cosmología, para formación de estructuras a gran escala en el universo, pero ésa posibilidad ya está descartada. No obstante su descubrimiento sería aún muy interesante. Por un lado son algo esencialmente nuevo, y éso siempre es importante. Más allá de éso su relevancia dependería del tipo de cuerdas que fueran. Sí son las que surgen cómo defectos topológicos entonces daría fé de la existencia de rupturas de simetría en el universo primitivo, que es algo requerido por las teorías de unificación. La primera ruptura de simetría está ligada al bosón de Higgs, y el descubrimiento de éste la ha confirmado, pero podría haber otras en las que un grupo SU(5), SO(10) o E(6) diera lugar al modelo standard SU(3)xSU(2)xU(1) y de ésos no hay noticia experimental a favor (y sí en contra de el SU(5) mas sencillo, que predice un decaimiento no observado del protón). Esas rupturas de simetría, dependiento de detalles de la topología (en los que no entraré aquí, básicamente relacionados con los grupos de homotopía de los grupos de Lie implicados) de los grupos implicados debería dar lugar de forma casi inevitable a la formación de cuerdas cósmicas. Éstas se pueden haber ido desintegrando con el tiempo, pero podrían quedar unas cuantas, y observar una demostraría, cómo dije la existencia de esas rupturas de simetría. Los experimentos de detección basados en un efecto mediante el cual se produce una duplicación óptica de lo que se ve inmediatamente detrás de una cuerda cósmica han fracasado hasta ahora y las ondas gravitacionales abren una posibilidad mejor de detectarlas.

Por supuesto sí se descubriesen cuerdas cósmicas que sean objetos de la teoría de supercuerdas agrandados a tamaños astrofísicos se tendría evidencia de la teoría de supercuerdas y éso sería el descubrimiento mas importante en física en los últimos 50 años, cuando menos.

Dejo algunos enlaces para ampliar detalles. Un artículo divulgativo sobre ondas gravitacionales y cuerdas cósmicas lo da la propia colaboración ligo ¿EXISTEN LAS CUERDAS CÓSMICAS?. Un artículo técnico muy reciente es Stochastic gravitational waves from cosmic string loops in scaling

Ondas gravitacionales y teoría de supercuerdas

A desarrollar en una próxima actualización.

Compactificaciones inhomogéneas y sus implicaciones físicas

Este año académico he estado leyendo mucho sobre compactificaciones, tanto a nivel de matemática pura (holonomía a fondo, espacios de moduli bastante a fondo y otras cosas bastante recientes de geometría analítica de las que creo que no hay aún nada o casi nada aplicado a la teoría de cuerdas) cómo a nivel de fenomenología, con la idea de trabajar en dos temas bastante concretos, uno puramente matemático y otro muy fenomenológico.

En el proceso, aparte de aprender sobre compactificaciones, he podido entender mucho mejor diversos aspectos de la teoría de cuerdas en general, y, en particular, todo lo de los móduli, que es un asunto bastante clave. También me ha influenciado un aspecto del LHC, el de las fluctuaciones estadísticas. En principio se supone que son sólo éso, pero entendiendo un poco la física de compactificaciones uno podría plantearse que a lo mejor las fluctuaciones tienen que ver con sucesos reales de nueva física, pero que desaparecen con el tiempo porque la física mas allá del modelo standard pueda no ser constante. Por supuesto a muy altas energías la física no variaría, y estaría dictada por la teoría de cuerdas. Sin embargo en regiones intermedias, entre el modelo standard y la energía de Planck, la teoría de cuerdas se manifiesta por, entre otras cosas, las compactificaciones y, tal vez, estas podrían no ser constantes en el espacio o en el tiempo, y, de esa manera, la física efectiva a esas energías intermedias podría no ser constante.

En esta entrada voy a exponer aspectos serios, al menos eso espero, sobre el asunto, y, al final, otros un poco mas exóticos, con consideraciones de un carácter mas anecdótico, aunque tal vez no del todo irrelevantes.

La idea parte de lo más elemental, la idea de Kaluza-Klein es relativamente sencilla de entender una vez se sabe relatividad general. La idea básica es añadir una dimensión espacial extra a las 3+1 del espacio-tiempo y hacer que esta sea un círculo. Sí en vez de 3+1 tomáramos 2+1 tendríamos un plano y a cada punto del plano le añadiríamos un pequeño círculo cuyo radio sería del orden de la longitud de Planck, o algo muy pequeño en cualquier caso. Matemáticamente podemos expresar éso cómo que tenemos un producto cartesiano de espacios topológicos 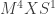(dónde 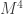es el espacio de Minkowsky en 3+1 dimensiones y 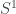es el círculo). Sí congelamos el tiempo, o aceptamos que la compactificación no varía con el mismo (que es lo que se suele hacer) tendríamos que el espacio es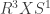

Los círculos de los diversos puntos se agrupan y dan lugar a un cilindro y la métrica de ese círculo, vista desde el espacio de 3 (2 sí estamos en el plano) dimensiones es la del electromagnetismo de Kaluza. Sí consideramos una partícula cuántica que pueda tener momento en la dirección de ese círculo ése estará cuantizado. Desde 4 dimensiones el momento en esa quinta dimensión se verá cómo una masa y una partícula, inicialmente sin masa,va a tener «copias» de diversas masas, múltiplos enteros unas de otras. Siendo relatividad general estamos trabajando con geometría diferencial intrínseca, y, por consiguiente, nos despreocupamos de cómo ese círculo, y el correspondiente cilindro, se pueden «encajar» en las dimensiones extra. También se asume normalmente que el radio del círculo es uniforme. Sí no lo fuera siempre podríamos decir que tenemos lo que se denomina una fibración con base el espacio de Minkowsky y fibra .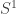

Las fibraciones son un tema matemático que requiere bastante esfuerzo introducir en detalle, y que requiere una buena base previa de geometría y topología a nivel de una licenciatura de matemáticas. De hecho es un tema para un quinto curso (algo que ya no existe en el plan de bolonia) o directamente para cursos de postgrado. Aún así la idea esencial no es terriblemente difícil de entender intuitivamente. Se trata de que a cada punto de un espacio denominado base B se le «pega» una copia de otro espacio F, denominado fibra. Juntando las fibras de todos los puntos se obtiene el espacio total, E, y hay una proyección 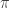que va del espacio E al espacio B que lleva cada fibra al punto del espacio B al que pertenece.

En cierto modo las fibraciones son una generalización del producto cartesiano y, de hecho, cuando la fibración es trivial el espacio total E es el producto cartesiano de la base por la fibra E=BxF, pero,en general, el asunto es mas complejo (aunque, localmente, el espacio sí que va a ser siempre un producto cartesiano dela base por la fibra, pero globalmente, en general, no) . Una forma muy sencilla de verlo es cuando el espacio base es un círculo y la fibra es un segmento. En ese caso el producto cartesiano es un anillo (un cilindro sin las tapas, vaya). Sin embargo en general no tiene porque ser así. Sí en cada punto del círculo la inclinación del segmento va cambiando el espacio total no va a ser ya un anillo. Un caso particular es cuando el último segmento está en la dirección opuesta al primero y se identifican ambos segmentos. En ese caso obtenemos la banda de Moëbius.

En las definiciones anteriores he sido muy impreciso. Normalmente se va a imponer que la fibra tenga alguna estructura extra. Por ejemplo sí F es un espacio vectorial vamos a tener un fibrado vectorial. Un ejemplo de éso sería el espacio vectorial tangente a una variedad. Sí la fibra es un grupo (normalmente un grupo de Lie) vamos a tener un fibrado principal. Hay un montón de estructuras extra que se pueden ir añadiendo al concepto de espacio fibrado, y, realmente, es una rama muy fecunda de la matemática, con múltiples aplicaciones a la física. Se puede, por ejemplo, formular una teoría gauge de grupo G cómo un fibrado principal con el mismo grupo. Los campos fermiónicos cargados bajo ese grupo formarían una fibrado vectorial asociado. ES un tema interesante y bonito, pero no es lo que me interesa tratar aquí. Hay libros de geometría y topología para físicos que hacen buenas y extensas introducciones al tema, cómo, por ejemplo, el de Nash y Shen o el Nakahara. También se pueden leer unas definiciones un poco mas formales en la wikipedia

Volviendo al tema de las compactificaciones, sí consideramos que el espacio base 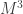, que no hay dependencia en el tiempo, y por tanto sólo nos importa la parte espacial del espacio de Minkowsky en tres dimensiones, tenemos que la base es 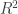. Si tenemos que el radio pueda variar de un punto a otro la fibra es 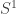. Hay que analizar ésto último con un poco mas de detalle si queremos ser rigurosos. Normalmente sólo se habla de espacios fibrados, al menos en geometria y topología diferencial, cuando son o bien fibrados vectoriales o bien principales. Posiblemente en física se suele ser mas descuidado y se admite como fibra «cualquier cosa» y cómo «fibrado» cualquier cosa que localmente es un producto, aunque globalmente no lo sea. Afortunadamente en este caso podemos ser «ortodoxos». Podemos ver que en el plano complejo (que topológicamente es equivalente al plano real) el círculo son los puntos de la forma 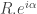siendo el producto de grupo la multiplicación de números complejos. Si R=1 tenemos el círculo unidad, pero, en general, para cualquier R (real) tenemos un círculo de ese radio. Por tanto podemos decir que nuestro fibrado es un fibrado principal. Cómo en la condición de fibrado nos preocupamos de que el espacio producto sea localmente un producto topológico, y en topología podemos cambiar libremente los tamaños, no pasa nada porque el radio varíe de un punto a otro.

Por supuesto toda esa consideración anterior sobre fibrados nos la podríamos haber ahorrado y dejar variar el radio del círculo sin mayores consideraciones. Realmente que algo sea un fibrado, en particular un fibrado principal, es útil porque se pueden crear espacios recubridores que caracterizan mediante clases topolóigicas (clases caracteristicas) los diversos espacios totales que se pueden formar con una base y una fibra dada. Dependiendo del tipo de grupo las clases serán de Stieffel-Wittney , de Chern o de pontryagin, y también éso puede ser útil en física de teorías gauge para tratar temas como los instantones y los solitones. Sí lo he incluido es porqué normalmente en la literatura física se trata el tema de forma muy descuidada y me parecía interesante dar algunas explicaciones al respecto.

Realmente el asunto del radio del círculo de la compactificación es un asunto delicado, incluso sí no nos planteamos que varíe en el espacio. En la teoría de Kaluza-Klein es un valor que viene dado y no está determinado por nada dentro de la propia teoría. Sin embargo las cantidades observables en el espacio ordinarios sí van a depender del radio de ése círculo. Por ejemplo, la constante gravitatoria en cuatro dimensiones estará relacionada con la de cinco por la relación 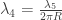y los valores de las copias K-K de una partícula van a tener masas 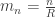. También la constante electromagnética va a depender del radio de ese círculo, y, en general, prácticamente todo ¡Y nada fija el valor de ése círculo!.

Durante bastante tiempo en la teoría de cuerdas nadie se preocupó demasiado del asunto. La primera persona, que yo sepa, que primero insistió en que había que ocuparse de ver cómo debería haber algo que fijara el tamaño de ése círculo fue un famoso crítico de la teoría de cuerdas, Lee Smollin. En terminología de cuerdas el radio de ése círculo es un «móduli» y fijar el tamaño del círculo es «la estabilización del móduli». El concepto de móduli lo introdujo Riemman, y, más o menos, viene a ser un parámetro, pero, desde luego, la historia es algo mas compleja que éso y la teoría de los moduli es muy rica, a la par que complicada, y no voy a entrar ahora a discutirla matemáticamente. En cualquier caso, usando «compactificaciones de flujo» se ha, más o menos, resuelto parcialmente el problema de la estabilización de los moduli en teoría de cuerdas, aunque al precio de introducir el landscape, pero bueno, ésa es otra historia. Un aspecto interesante es que en las compactificaciones tipo flux,el flujo que les da nombre es un flujo de unos campos antisimétricos (representables mediante formas diferenciales) que están en el espectro de la teoría de cuerdas que son unos análogos mas generales del campo electromagnéticos. Las fuentes de ésos campos van a ser D-branas. Sí uno considera el campo gravitatorio de una D-Brana va a obtener que el espacio-tiempo alrededor de la D-brana va a ser un «braneworld» a lo Randall-Sundrum, y va a estar «warped» (algo así cómo retorcido). Esos espacios warped ya no van a tener estructura de producto cartesiano, incluso aunque el valor de los moduli no varíe y, por tanto, tampoco va a ser una fibración cómo la que expliqué antes.

En la resolución habitual del problema de los móduli el valor del móduli, en éste caso de el radio del círculo, es la misma en todo el espacio-tiempo, aunque no es imposible buscar casos en que ésto no sea así. En general, en teoría de cuerdas, la historia es mas compleja y las compactificaciones tienen muchos moduli. Podemos entender intuitivamente que el móduli es un parámetro que nos indica cómo podemos modificar un espacio para que cambien algunos aspectos del mismo, pero sin afectar la estructura fundamental del mismo. En el caso del círculo el único moduli es el radio. En el caso del toro, que hay dos círculos, tenemos un moduli que seria el cociente del radio de los dos círculos (y que daría toros mas gordos y toros mas fínos) y otro algo más sutil de entender que no explicaré. En general, para una compactificacion típica de Calabi-Yau, de tres dimensiones complejas, el espacio de moduli es muy amplio, y, además, se descompone en dos partes: modulis de forma, y módulis de tamaño. La física en las 4 dimensiones va a depender de muchos aspectos de ésos Calabi-Yaus. Alguna va a depender propiedades independientes de los moduli, cómo por ejemplo el número de familias de partículas (que va a ser igual a la constante de Euler de el Calabi-Yau para la cuerda heterótica, y a los números de intersecciones de los ciclos de Calabi-Yaus en que se enrollan las D-branas en las cuerdas tipo II B, por sí tenéis curiosidad y sabéis más o menos de que hablo xD). Otras propiedades, por contra, sí van a depender de los móduli. Aparte de los moduli hay otro campo, el dilatón, que va determinar la fisica de las 4 dimensiones. Normalmente el valor del dilatón no varia en el espacio, pero hay compactifícaciones en las que sí (y en teoría F se combina con un axión formando el axio-dilatón, que es un fibrado elíptico y, por tanto, de manera natural varia).

Éso lleva a que uno debería plantearse que pudiera darse el caso de que la física en cuatro dimensiones pudiera depender del punto del espacio, y, si acaso, que variase en el tiempo. Hay limitaciones experimentales muy serias sobre las posibles variaciones de las propiedades (por ejemplo masa) partículas del modelo standard y sobre los valores de las variables de acoplo gauge y no parece que varíen en absoluto. Pero podría ser que la física mas allá del modelo standar sí lo hiciera. Cómo no conocemos física mas allá del modelo standard no tenemos noticias al respecto. Pero sería muy interesante especular con las implicaciones de que fuera variable. En ese caso las masas de las partículas no osbervadas, y las secciones eficaces de producciones de las mismas, podrían variar en el tiempo o el espacio. En realidad, dado que la tierra se mueve, sí solo varían en el espacio, desde el punto de vista de la tierra sería cómo si variasen en el espacio. Éso sí, las variaciones no serían totalmente al azar sino que estarían determinadas por la teoría de cuerdas y unas variaciones estarían correlacionadas con otras. Por otro lado sería natural que esas variaciones tuvieran algún tipo de estructura periódica. En ese caso podría ocurrir que una partícula, en un instante dado, tuviera una alta sección eficaz de producción, y apareciera cómo una desviación estadística en el LHC. Pero, según la tierra se mueve (o el tiempo avanza) su sección eficaz de producción bajaría y parecería haber sido una mera fluctuación estadística. El caso es que, sí es la física 4d, que depende del espacio-tiempo al ser la compactificación no constante en el mismo, si supieramos, más o menos, que compacticiación tenemos, podríamos saber que sí han aparecido unas fluctuaciones A y B entonces deberían aparecer otras, C y D, y que, luego, en otro momento volverán A y B.

Realmente el tema de las compactificaciones variables ha sido tratado en la literatura, pero de manera muy dispersa. En cosmomlogía Kolb, en 1986, consideró compactificacoines toroildales con radios variables, pero no se obtuvo nada útil (se puede ver una introduccion al tema en el capítulo de cosmologías en dimensiones extra del libro de Collins-Martin-Squires «particle physics and cosmology). Realmente es difícil dar en la literatura con algo al respecto. Unos autores, por ejemplo, han considerado algo parecido, en modelos con D-Branas, en las que la posición de unas D-branas varían de un punto a otro, y lo llaman «soft branas». Un articulo reciente que trata el tema es Inhomogeneous compact extra dimensions. En todo caso ninguno de los artículos que he encontrado plantea el tema de la forma que lo he expuesto aquí, es decir, analizando las consecuencias para el LHC en forma de «partículas de Cheshire», que, cómo el gato de Cheshire, aparecen y desaparecen cómo si fueran fluctuaciones estadísticas. Tengo muy perfilado un artículo en el que basándome en un modelo de intersecciones de D-branas en ciclos de Calabi-Yau, considerado cómo modelo genérico para predicciones de cara al LHC de éste tipo de escenarios de teoría de cuerdas, permito que el dilatón varíe en el espacio, y así obtener unas predicciones, también, genéricas de cómo podría variar el asunto. Realmente sería mas interesante ver sí alguno de los modelos propuestos para el famoso LHC bumb a 750 GeV, que apareció a 4.X sigmas, y luego se desvaneció, puede encuadrarse en una compactificación variable y ver sí esa fluctuación se puede haber ido a algún otro sítio (o sítios) en los que también darían alguna pequeña fluctuación observable y, en ése caso, se tendría una predicción basada en teoría de cuerdas para el LHC. Obviamente el asunto es muy complicado, y requiere manejar muchos aspectos de fenomenología, cómo encontrar el superpotencial, encontrar cómo se rompe la supersimetría por ese superpotencial, la masa de las partículas resultantes, y cómo esa masa depende de los móduli, y lo mismo para las secciones eficaces de las partículas con esas masas. Mucho me temo que, aunque conozco la materia, no tengo la soltura para obtener los cálculos detallados con demasiada presteza. Afortunadamente tengo ideas para otras cosas que requieren menos tecnicismos tan extensos :).

Tal vez es muy optimista pensar que las variaciones sean sustanciales en las distancias que pueda recorrer la tierra en el periodo de unas horas o incluso años. Tal vez haya fluctuaciones, pero sólo a muy gran escala. En ese caso habría también consecuencias posibles. En el escenario WIMP para la materia oscura normalmente ésta va a ser el LSP (partícula supersimétrica mas ligera). Pero sí la masa de esa partícula varía de una zona a otra del espacio, y esas partículas, o las que terminaron decayendo en esa partícula, se formaron muy al inicio del universo, entonces la partícula LSP (o en general, las que formen la materia oscura) podrían tener masas diferentes en diferentes zonas del universo. Éso sí, por diversos procesos se habrán podido ir mezclando unas con otras y, en el universo actual, habrá, en una zona dada, partículas de materia oscura que provengan de diversas zonas del universo y que, según ese esquema, tendrán diferentes masas para el mismo tipo de partícula. Cómo los experimentos actuales buscan una partícula que siempre va a tener la misma masa entonces es muy probable que fallen en su búsqueda, que, de hecho, es lo que está pasando. Obviamente hay muchos motivos por los que puede fallar esa búsqueda que no sea éste, pero quizás sería interesante plantearse sí hay modificaciones de los experimentos que puedan tener en cuenta escenarios de este tipo.

Hasta ahora todo lo que he escrito es bastante serio y relativamente ortodoxo. Voy ahora con la parte menos seria, que se me ha ocurrido al analizar lo anterior. Una de las cuestiones sobre la estabilización de los móduli es que habría que plantearse cómo el valor que tome en un punto va ser igual al que tenga en otro punto. He dicho que los moduli los van a fijar los flujos, pero no he dado todos los detalles. Un aspecto muy molesto en la literatura física es que cuando se habla de móduli muchas veces se dice que estos son campos escalares. De hecho los moduli no sólo aparecen en teoría de cuerdas sino en vacíos de teorías de campo supersimétricas, o en los espacios de móduli de los instantones de las teorías gauge, y, dado que en teoría de cuerdas también hay instantones, pues hay un moduli space de instantones (que suelen hacer contribuciones no perturbativas a los potenciales). Hay todas esas acepciones y no siempre se tiene muy claro de que habla el autor. En todo caso, así, en líneas generales, el esquema es entendible. El móduli, como digo, es un parámetro que indica las deformaciones de una estructura geométrica (o una familia de estructuras geométricas). Un toro es una estructura geométrica, pero un toro concreto tiene unos radios y ángulos entre los círculos determinados. Bien, las deformaciones que llevan un toro a otro están dados por los moduli. Un toro, por cierto, es también una estructura de Riemman, es decir, una variedad compleja de dimensión, compleja, uno. Al espacio de moduli del toro también puede dársele estructura de espacio complejo, aunque, en general, los espacios de móduli van a tener algún tipo de singularidad. Bien, éso es la matemática del asunto. En física, en general, lo que va a ocurrir es que vamos a tener una compactificación, en la que van a vivir una serie de campos. Se puede calcular (hay fórmulas relativamente tratables para ello) la dimensión del móduli space en términos de clases características y, en última instancia, de los números de Betti del espacio de la compactificación . Resulta que, en general, para cada móduli geométrico la teoría de cuerdas nos va a dar un campo escalar. Pues bien, los flujos lo que van a hacer va a ser generar un potencial para ése escalar y, se supone, el campos va a ir al mínimo de ése potencial y, de ese modo, queda fijado el moduli correspondiente.

Bien, entonces una vez que entendemos que el móduli va estar asociado al al valor del mínimo del potencial de un campo escalar ya podemos empezar a plantear mejor la cuestión de cómo podría de ser ése mínimo distinto de un punto a otro. El caso de un campo escalar que toma un valor de mínimo existe en física ¡es el bosón de Higgs! Se supone que el bosón de Higgs estaba en un máximo inestable y, en un momento dado, en algún punto del espacio, cayó a un valor concreto de mínimo. Había un continuo valores posibles para el mínimo. Cómo el Higgs se puede mover en las 3 dimensiones espaciales se supone que una vez tomó el mínimo en un punto transmitió el valor al resto de puntos de las 3 dimensiones (una esfera de nuevo vacío expandiéndose a la velocidad de la luz).

Ahora bien, sí un campo escalar de moduli tuviera, por lo que fuese, varios posibles para el mínimo (hay potenciales con mas de un mínimo, vaya) y en un punto del espacio toma valor en uno de esos mínimos ¿puede transmitir ese valor a los puntos colindantes, y, en última instancia, a todo el espacio? Dado que el campo vive sólo en las dimensiones extra no puede (o no es obvio que pueda) transmitir ese valor a través del espacio 3d ordinario.

Pues bien, ahí es dónde entra el tema «poco serio», puras especulaciones mías un tanto descabelladas posiblemente, que voy exponer ahora. En las imágenes mentales de Kaluza-Klein se pinta, cómo ya dije, que la dimensión extra es una «manguera muy estrecha» sobre un plano. Es decir, se supone que los círculos de cada 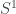toman la misma orientación en todos los puntos del espacio y forman un cilindro. Ahora bien ¿En que dirección? Es decir, podemos coger una línea paralela, por ejemplo,al eje x, y adosar un cilindro a cada una de esas líneas. Pero también podrían estar adosadas al eje y. O, otra posibilidad, es que la orientación de los círculos fuera variando y se cerrasen sobre un círculo dibujado en el plano.

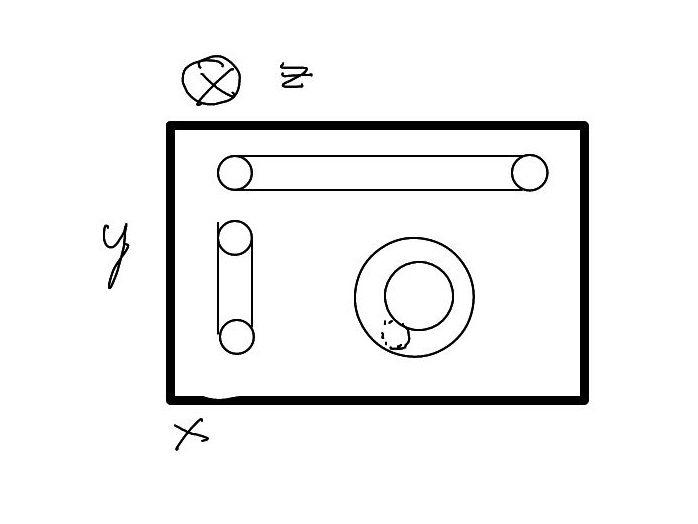
No tengo claro sí habría alguna consecuencia para la física «del plano» que dependiera de la orientación de los cilindros (aparentemente no, porque en relatividad general hablamos de geometría intrínseca, que no debería depender de ese aspecto, pero no estoy 100% seguro), pero, sin entrar en éso, ya tenemos un posible problema. Sí, cómo he razonado, parece plausible que el valor del móduli (el radio del círculo) surja de que un campo escalar, que vive en uno de los círculos, tome un valor de un potencial, que depende de la geometría interna de ése círculo, y ese potencial tiene varios mínimos posibles, entonces podría transmitir ese valor a los círculos de ese mismo cilindro, pero no está claro que dos cilindros paralelos se puedan comunicar entre si, y, por tanto, que dos cilindros paralelos deban tener el mismo valor del radio. En el caso de que los círculos se cierren formando un toro el asunto es aún peor pues cada zona del espacio podría tener su propio valor. Mas grave sería que cada círculo tuviera una orientación al azar, o que se agruparan por domínios, al estilo de los spines de los imanes.

Entonces una cuestión natural es ¿Hay varios valores posibles para los mínimos? Bueno, el valor del potencial lo fijan los flujos, y para ésos sí hay muchos valores posibles. Los flujos tienen valores cuantizados, pero hay una enorme cantidad de valores posibles. Hay un valor arquetípico 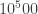. Realmente ese es el problema del landscape, que hay muchos valores posibles, compatibles con el modelo standard (o con la constantes cosmológica). Se supone que, de hecho, hay saltos posibles de unos valores a otros de manera espontánea y que éso resolvería el problema de la constante cosmológica. Por supuesto se supone que los flujos son los mismos en cada punto del espacio-tiempo, dentro de un mismo espacio del multiverso, pero, igualmente, podría ser que hubiera una dependencia del flujo de un punto a otro (aunque ésto lo tengo menos claro).

Otro aspecto muy curioso es el siguiente. Realmente un círculo requiere dos dimensiones. Si decimos que estamos compactificando a un círculo tenemos que asumir que hay dos dimensiones extra. Si, cómo hacemos en los dibujos, pintamos el círculo encima de una recta entonces tendremos que para dos rectas paralalas que estén a una distancia menor que el radio del círculo los cilindros de cada recta se solaparían unos con otros. Si consideramos el caso de «dos dimensiones extra», y una compacticiación en un toro, para cada circulo deberíamos tener dos dimensiones, dando lugar a 4. En realidad la cosa es un poco más compleja, porque podría tal vez haber alguna forma de acomodar ese toro de alguna manera que no requiera cuatro dimensiones. Por «acomodar» habría que especificar tecnicamente lo que queremos decir. Matemáticamente éso nos lleva a dos conceptos posibles que plasman la idea, la inmersión y el embedimiento (embbeding) cuyos detalles no voy a dar. El concepto mas fructífero y adecuado posiblemenente el embeding, y hay un teorema que nos dice que una variedad suave de dimensión n se puede, en el peor de los casos, embeber en un espacio 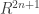. A priori ésto no es un problema, pero, sí asumimos que estamos en un mundo que viene de la teoría de cuerdas, y éstas tienen originalmente 10 dimensiones, y se termina con 4 dimensiones extensas y 6 compactificadas, uno podría pensar que la variedad que está compactíficada debería también ser embebible en 6 dimensiones. Pero, claro, en todo este tiempo hemos dicho que las compactificaciones tienen como base el espacio de Minkowsky, pero, obviamente, éso no es el mundo real, que es un mundo curvo, por aquello de que cualquier masa curva el espacio. Incluso a gran escala, dónde podemos suavizar y considerar irrelevantes las fluctuaciones de curvatura de cuerpos astrofísicos, tenemos que, en su conjunto, el espacio es mas bien una esfera en expansión, y, si damos por bueno que hay una constante cosmológica, es, concretamente, un espacio de de Sitter. Y ése espacio no se puede embeber en un 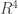asi que ya vamos cortos de dimensiones. Por supuesto todo ésto que he dicho es irrelevante porque, fuera de las dimensiones de la teoría de cuerdas, no tiene sentido hablar de geometría y no deberíamos preocuparnos de en que embeber los espacios internos. Es obvio sí uno reflexiona sobre ello, pero no del todo inmediato, y, desde luego, no es algo que uno vaya a ver discutido en ningún libro serio, pero, tal cómo yo lo veo, ésa es una función de los blogs, poder discutir también cuestiones curiosas, y naturales, aunque no sean del todo serias ;-).

Por cierto, aunque a esto de los embeding y las imágenes mentales lo he presentado con un tono mas anecdotico que serio lo cierto es que no es un asunto trivial. En el libro que he mencionado, Particle Physics and Cosmology , los autores mencionan que el mecanismo de Kaluza tiene un pequeño problema debido a que la curvatura gaussiana de un cilindro es nula. Es fácil de entender porque es ésto. La curvatura gaussiana Cg en un punto es el producto de la curvatura máxima y la mínima de entre las curvas embebidas en la superficie Cg=Cmax*Cmin. En un cilindro la curvatura máxima es la del círculo que pasa por el punto, y la mínima la de la recta que pasa por ese punto. Cómo la curvatura de una recta es 0, Cg=Ccírculo*0=0. Por supeusto ésto da carta de naturaleza a que hay que «tomarse en serio» la imagen mental del cilindro, pero, en ése caso tenemos que tomarnos también en serio las consideraciones sobre la orientación de ésos cilindros, o porqué cilindros y no toros, etc, etc.

En fin, es una entrada larga, y dura en muchos aspectos, espero que se haya entendido algo. Tengo previsto escribir pronto sobre las teorías unificadas de Einstein, pero cómo estas incluyen Kaluza-Klein, me pareció oportuno comentar estas reflexiones exóticas sobre ese tema que se me han ido ocurriendo este año. De hecho, la parte de la física mas allá del modelo standard que pueda ser no constante en el espacio y tiempo, posiblemente sea mucho mas interesante, dentro de la ortodoxia cuerdista actual, que las teorías de unificación de Einstein, que es algo que he estudiado sólo por influencia de la serie Genius 🙂

Einstein y la mecánica cuántica: mas allá de dios y los dados

En el post anterior anunciaba que había leído el libro que se muestra en la imagen Einstein’s Unification, escrito por jeroen van dongen, y que pensaba escribir sobre el mismo, y sobre parte de lo que he sacado de ése libro va esta entrada. Aunque el libro analiza las teorías de unificación, a lo largo del mismo, y, sobre todo, en el capítulo final da una visión de la relación de Einstien con la cuántica, que es de un interés independiente.

Aunque todo el mundo reconoce a Einstien cómo un genio, posiblemente el mejor físico de la historia después de Newton. Sin embargo se tiene la idea mayoritaria de que tuvo un «año mirabilis», el 1905, dónde publicó las ideas de la relatividad especial, incluyendo la equivalencia entre masa y energía, el efecto fotoeléctrico y el movimiento browniano, que luego pasó 10 años hasta crear su gran logro, la relatividad general, pero no demasiadas cosas más, y que, a partir de ahí, su aversión a la mecánica cuántica le alejó de la investigación puntera y que se dedicó a su cruzada anti cuántica, sobre todo en sus debates con Bohr, ejemplificada sobre todo en su trabajo con Podolsky y Rosen, la paradoja EPR, y, por otro lado, en una búsqueda inútil de una teoría unificada, abocada totalmente al fracaso desde el principio, y sin ninguna influencia posterior.

Pues bien, viendo la serie, leyendo éste libro, indagando referencias (véase por ejemplo el muy interesante artículo Del efecto fotoeléctrico (1905) a la condensación de Bose-Einstein (1925).Un curioso ejemplo de simbiosis en el desarrollo de teorías físicas. ) y reflexionando un poco sobre cosas que uno estudia en la carrera se da cuenta de que esa percepción es bastante errónea.

Lo primero es deshacer un mito. Einstien nunca dijo la frase «Dios no juega a los dados». La frase exacta, extraida de una carta a Max Born, es: “La mecánica cuántica es ciertamente impresionante. Pero una voz interior
me dice que no constituye aún la última palabra. La teoría explica muchas cosas,
pero realmente no nos acerca más al secreto de “El Viejo” [sic]. Yo, en cualquier
caso, estoy convencido de que Él no juega a los dados.”

ES similar, pero difiere en un matiz muy importante. Podría pensarse que «el viejo» es una entidad divina, sí uno tiene tendencias religiosas, pero también podría pensarse que es una palabra para referirse a la naturaleza, así, en un sentido amplio, de el mundo natural y sus leyes físicas, y, en ése caso, no tendría connotaciones religiosas y no sería adecuado traducirlo por «dios». Por todo lo que se sabe de Einstein no era una persona particularmente religiosa, mas bien era agnóstico o ateo, al menos la mayor parte de su vida.

Dejando aparte esa curiosidad hay aspectos mucho mas interesantes sobre la relación de Einstein con la cuántica. Para empezar Einstein hizo contribuciones fundamentales a la cuántica. Su explicación, en 1905, de la ley de Planck, relacionada con el efecto fotoeléctrico (aunque en el artículo original analizaba la ley de Wein y sólo cómo un ejemplo trataba el efecto fotoeléctrico) y que le acabaría valiendo el nobel, fue el primer paso hacia la idea cuántica. Mas adelante, en 1916,un año después de elaborada la relatividad general, abundó al respecto y presentó la idea del fotón. La forma en que se expone ahora el efecto fotoeléctrico en los capítulos de física moderna de la enseñanza secundaria dan a entender que se hizo todo a la vez, y con una matemática muy elemental, pero claramente no fué así.

También en su modelo del sólido en 1907, posteriormente perfeccionado por Debye, introdujo vibraciones atómicas cuantizadas, y, mediante esa teoría dió una explicación al calor específico de los sólidos en la que éste no dependía unicamente de los electones, que daban una contribución proporcional a la temperatura T, sino una debida a los nucleos, y que daban una proporcional a .

Mas adelante, en 1909, introdujo el concepto de la dualidad onda-corpúsculo. Esa idea de la dualidad onda corpúsculo influyó para que de Broglie creara su teoría de las ondas de materia. Realmente de Broglie tuvo otras influencias, la de la teoría cuántica primitiva, con el modelo atómico de Bohr y las reglas de cuantización (osea, las únicas órbitas posibles de e un electrón son las que tienen una circunferencia que es un múltiplo entero de la constante de Planck, y posteriores generalizaciones de Sommerfeld usando variables de acción-ángulo). La idea que movió a de Broglie es que esos valores cuantizados se debían a que debía haber una onda estacionaria, y, por tanto, tenía valores discretos de la energía, aunque no llegó a dar una formaexacta de la ecuación de onda, éso vendría mas tarde. Hay que decir que el propio Einstein contribuyó en cierta manera a la idea de las reglas de cuantización y hay gente de la época que habló con él que dice que es bastante probable que él mismo creara un modelo atómico equivalente al de Bohr, aunque no llegaría a publicarlo.

Recordemos, y ésto es importante, que toda esta primera mecánica cuántica, anterior a la ecuación de Schröedinger, y a la formulación matricial de Heissenberg, no era probabilística. Recordemos también que la susodicha ecuación, y las ideas de Heissenberg, son de 1925, es decir, 10 años posteriores a la relatividad general. Obviamente Einstein no podía tener ningún problema en esa época con una interpretación probabilística que ni siquiera existía, y que, de hecho, es del 1926, un año posterior a la ecuación de Schröedinger. Curiosamente sí a ello vamos, el primero que introdujo conceptos probabilísticos relacionados con la teoría cuántica fué ¡el propio Einstein!. En un artículo escrito en la época entre 1915 y 1925 (que ya vamos viendo que fue una época muy productiva, nada que ver con la idea de que después de la relatividad general Einstien no hizo nada especialmente útil) publicó una nueva deducción de la ley de Planck, de una manera mucho mas elaborada y cercana a las leyes de la mecánica estadística de Boltzman. Para hacerlo tuvo que introducir probabilidades en los ángulos de emisión de los fotones, algo que no le gustaba, pero que funcionaba.

Pero, vamos al grano, sí esa primera mecánica cuántica no era probabilística, y él mismo contribuyó a ella conceptualmente de forma muy decisiva ¿Por qué los físicos cuánticos de esa época ya no le contaban cómo «uno de los suyos»? La clave es que el desarrollo de la cuántica no es cómo se pinta en (al menos la mayoría de) los cursos de introducción a la misma. Ahí se introduce, tras una exposición rápida y somera de las ideas de la cuántica antigua, el formalismo de función de onda, los operadores de posición y momento (cuya expresión se obtiene de manera heurística a partir del comportamiento de un paquete de ondas), el hamiltoniano en términos de ésos operadores, la teoría de perturbaciones, que permite obtener aspectos finos de los espectros cuánticos, y todos los resultados se obtienen en ese formalismo, incluyendo cosas cómo las relaciones de incertidumbre de Heissemberg (relacionadas con la no conmutación de los operadores ).

Pero la realidad histórica es muy diferente. Prácticamente todos los resultados sobre espectros cuánticos se obtuvieron antes de 1925 de forma experimental y se fueron obteniendo reglas ad hoc que los explicaban. Incluso algo cómo el principio de exclusión de Pauli (dos partículas cuánticas de spin semientero no pueden estar en un estado con los mismos números cuánticos) se obtuvo de forma experimental antes del formalismo de función de onda. Es curioso porque en éste formalismo, introduciendo los espinores de pauli y la teoría del spin, se deduce de manera fundamental, pero la idea inicial de la misma fué para explicar experimentos.

Incluso la formulación matricial de Heissenberg tuvo una componente muy experimental, algo conocido cómo el principio de combinación de Ritz para la adición de frecuencias de luz emitidas cuando un electrón de cae de un estado na aun estado k, combinado con una descomposición en modos de Fourier de la teoría clásica del movimiento de un electrón alrededor de un átomo de acuerdo a ésta regla.Un aspecto clave, a nivel conceptual, es que Hissenberg adjudica matrices (operadores lineales sobre un espacio de Hilbert) y los relaciona, sí son autoadjuntos, con cantidades observables, lo que se conoce cómo el principio de correspondencia, pero es algo que se postula, sin ninguna justificación obvia.

Pues bien, es esta característica de leyes inmediatas, sin gran justificación conceptual, postuladas ad hoc para explicar resultados experimentales, lo que molestaba a Einstein. Él, en su momento, había tenido simpatía por la física experimental y los laboratorios. Pero, por una lado los laboratorios se iban haciendo cada vez mas sofisticados, y había que especializarse mucho para poder hacer algo útil en uno, y, más importante, en su desarrollo de la relatividad general inicialmente había tenido un balance entre influencias experimentales, otras conceptuales y otras puramente matemáticas. En las diversas etapas de desarrollo algunas ideas de contenido muy físico y experimental le habían llevado a ecuaciones equivocadas, y solamente cuando se guió por la elegancia matemática, el principio de covarianza básicamente, obtuvo las ecuaciones correctas. Éso, y posiblemente un rechazo a los físicos nazis que tanto le importunaban, muy cerraditos en la experimentación mas básica y sin nada de imaginación ni sofisticación matemática o conceptual, le hacia sentirse a disgusto con esas ideas. De hecho, al menos según la serie, a Einstein siempre la motivaba saber la explicación última desde el principio de su carrera. En ése sentido es natural que se sintiera a disgusto con la cuántica primitiva pre Schróedinger. La mecánica matricial, aunque algo mas formal, tampoco le parecía una teoría completa porque postulaba la cuantización, pero no la deducía, y él quería una teoría en que la cuantización se dedujera de algo mas fundamental. Otra incomodidad con esa formulación es mas anecdótica, pero reveladora, y merece la pena comentarla.

En la enseñanza actual apenas se ve la formulación matricial. Se explica que los operadores, en una base dada del espacio de Hilbert, van a ser matrices, de dimensión infinita. Obviamente cómo en general el producto de dos matrices no es conmutativo dos operadores en general no van a conmutar. Pero el caso es que casi nunca se ven esos operadores cómo matrices infinitas, Lo que se ve es que son operadores diferenciales (caso del momento) o de mmultiplicación por una variable (caso de la posición) actuando sobre la función de onda, que es éso, una función matemática. Esa introducción heurística de los operadores posición y momento es demasiado liviana para el gusto de Einstien que querría obtener el principio de correspondencia de una forma mas fundamental. Y sí, sabemos que la función de onda puede ser escrita cómo combinación lineal de autofunciones del operador hamiltoniano. Siendo el hamiltoniano un operador autoadjunto la teoría de Sturm-Liouville nos dice que (para espectro discreto) va a tener una serie de autofunciones que son base de un espacio de Hilbert. Mas abstractamente se puede usar el análisis funcional y ver que la teoría de Sturm-Liouville es el caso de un operador compacto y éstos tienen espectro discreto y sus autofunciones forman un conjunto completo (teorema de representación de Riesz, sí no me falla la memoria). en realidad, sí somos estrictos, la cosa es mas complicada porque el operador hamiltoniano no es compacto, y tenemos que usar la teoria de espacios de Hilbert equipados y demás).

Pero, realmente, muchas veces tenemos una expresión explícita para la ecuación de onda y podemos olvidarnos de todos esos «tecnicismos» y no se piensa demasiado en los operadores cómo matrices infinitas. Sin embargo, en la primera versión de Heismberg sí se usaban. Y ahí está lo que me llama la atención. La métrica de la relatividad general es «una matriz». El tensor de Ricci «Es una matriz» y el propio tensor de Einstein es «una matriz». Es decir, sí fijamos un sistema de referencia coordenado éstos tensores son matrices. El caso es que en los sistemas actuales el álgebra matricial se enseña desde secundaria, y en primero de carrera hay un curso de álgebra lineal, y cualquier estudiante de ciencias se maneja perfectamente con matrices. De hecho dónde muchos tienen dificultades es con el concepto de tensor, en cualquiera de sus definiciones. En época de Einstien, deduzco, el cálculo tensorial de Levi-Civitta no debía hacer uso de notación matricial porqué en un momento dado describe la multiplicación de matrices cómo «unas reglas de brujería» y, por lo visto, hay evidencias de que, al menos en algún momento temprano de la nueva mecánica cuántica, manejó incorrectamente esas matemáticas.

Pero vale, entonces Einstein estaba incomodo con la cuántica primitiva porque era demasiado «experimental» y «vulgar». Pero la nueva mecánica cuántica sí era una teoría muy elegante y muy formalmente clara, con unos principios muy bien establecidos, pero aún así no le gustaba. Se suele tener la idea de que su gran disconformidad provenía de la probabilidad, pero, como vamos a ir viendo, el asunto es bastante mas complejo.

Recordemos que, incluso antes de la introducción de la interpretación probabilística, hay un aspecto que parece irrelevante: la función de onda de un sistema de n partículas depende de las coordenadas de esas n partículas . ¿Obvio verdad? ¿Que problema puede haber con ésto? Pues, en realidad, sí lo hay, al menos desde la perspectiva de Einstein. La cuestión es que Einstein, más o menos,consideraba aceptabable la idea de «ondas de materia» de de Broglie, que, más o menos, es igual en la teoría de Schröedinger, al menos en la interpretación no probabilística (osea, una especie de densidad de carga). De hecho su propio principio de dualidad onda-corpúsculo queda bien plasmado en esa idea. Pero para que éso sea acorde a su idea física cada partícula debe tener su propia onda, no puede ser que haya una única función de onda para todas las partículas porque éso arruina buena parte de la interpretación física que él apoya (de hecho la famosa paradoja EPR y el realismo posiblemente tengan mas que ver con ésto que con la probabilidad en sí).

De hecho la probabilidad sólo se manifiesta en la paradoja EPR por culpa de la función de onda conjunta. Al producirse el «colapso» de la función de onda esa función de onda conjunta da lugar a la «acción fantasmal a distancia» (una partícula transfiere – o éso parece, aunque no es así realmente- información a otra situada a una distancia arbitraria) que va en contra del principio de realismo, y, en última instancia «en espíritu» (aunque no en forma) contra la idea de Einstein de causalidad, relacionada con la relatividad especial. Posiblemente sí la interpretación probabilística de Born se aplicara a una función de onda de una única partícula yo creo (pero obviamente no tengo manera de saberlo xD) que Einstein podría aceptar mas o menos la idea. El problema es que al tener una función de onda de dos o más partículas parece cómo sí esas partículas pudieran comunicarse entre sí a una distancia arbitraria. Y digo «parece» porque creo que Einstein no comprendía del todo bien el entrelazamiento cuántico. De hecho yo mismo, influenciado por la formación que he tenido, mucho mas reciente que la suya, he llegado a descubrir que tenía una visión muy pobre e incorrecta del mismo y que, definitivamente (cómo he visto sugerir a Sean Carrol en su facebook) hace falta un libro de texto que trate el tema con mas rigor y así se evitará que la gente tenga ideas obvias e inmediatas, pero falsas, respecto a las implicaciones y posibilidades del entrelazamiento, pero ésa es otra historia, claro. Quizás con los desarrollos modernos en el entendimiento del entrelazamiento Einstein podría sentirse algo más a gusto con esa idea de la función de onda conjunta, pero diría que, incluso a´si no del todo.

Por cierto, la función de onda debe ser una función compleja (de variable real). En la gran mayoría de problemas que se resuelven en la carrera siempre se va a obtener una solución con una función real, salvo en el caso de los procesos de colisión, dónde es una onda compleja, pero éso incluso en física clásica se usa a modo «formal» y por tanto pasa un poco desapercibido, pero, realmente, que la función deba ser compleja tiene una importancia fundamental y posiblemente arruine un poco la idea mas «física» de la interpretación de «ondas de materia» de de Broglie y Schröedinger con la que comulgaba Einstein, pero éso es un tema sobre el que no he leído nada.

Bien, ésto es lo que comenta jeroen van dongen al respecto, pero, una vez lo leí me surgieron preguntas. Por ejemplo, en la carrera se estudia la estadística cuántica de partículas bosónicas o «estadística de Bose-Einstein». Ahí se explica que la función de onda de varias partículas debe ser simétrica bajo el intercambio de las coordenadas de esas partículas. Pero acabo de explicar que Einstein no aceptaba la idea de una función de onda que agrupara partículas entonces ¿Cómo es que puede estar el nombre de Einstein en una estadística cuántica, cuando a él no le gusta la cuántica en general, ni la base microscópica de esa estadística en particular?. La respuesta está en el artículo de Luis Navarro Veguillas que enlacé antes. Procedo a pegar (parte de) la explicación que ahí viene:

El joven físico bengalí Satyendranath Bose (1894-1974) publicó en 1924 un
trabajo –traducido por Einstein al alemán y recomendado para su urgente publicación–
en el que, por primera vez, se deducía la fórmula de Planck de una forma
verdaderamente independiente del electromagnetismo clásico28. A cambio se hacía
pleno uso del concepto de fotón y de la hipótesis de que sus estados no estaban
asociados a los puntos del espacio de las fases, sino a regiones de éste –celdas– de
volumen finito, de valor h
3
.
La deducción pasaba por una original forma de distribuir los fotones entre las
celdas, para calcular la probabilidad de un estado. Introducida dicha probabilidad en el
principio de Boltzmann se obtenía la entropía de la radiación, de la que se deducía sin
dificultad –tras la imposición de la condición de equilibrio como estado de máxima
entropía– la fórmula de Planck para la radiación. Hoy diríamos que la idea de Bose
consistió simplemente en tratar a los fotones como partículas indistinguibles. Pero la
terminología no sólo resulta anacrónica, sino que conduce a una idea falsa del contexto
en el que se produjo la aportación de Bose quien, según propia confesión, nunca fue
consciente de que su tratamiento representara una innovación, pues siempre pensó que
actuaba plenamente dentro de la más pura ortodoxia de Boltzmann:
29

Entonces ya se ve que los problemas de Einstein con la cuántica son mas fundamentales que la probabilidad. Le parecía que la cuántica una idea poco fundamentada. Sí, tenía unos postulados, y a partir de ahí era consistente, pero él buscaba una teoría mas fundamental. Curiosamente, según he intentado hacer ver, quizás la parte grave no es que esa teoría tuviera que ser determinista. Por ejemplo, en un momento dado, a Einstien le exponen una teoría de variables ocultas, osea, que hay variables extra que hacen que, sí se supieran esas variables, la cuántica fuera determinista, pero no les hace demasiado caso, y, de hecho, no le gustan y no ven que cumplan los requisitos que él busca en su teoría mas fundamental.

Esa teoría debería permitirle obtener, por ejemplo, el valor de la constante de Planck, pero también debería explicar porque debería haber unos operadores ( y el principio de correspondencia entre observables clásicos y operadores) y el resto de los postulados. En una parte del libro comenta que tenía algunas ideas de por dónde debería ir el asunto. Por ejemplo van dongen cita que Einstein pensaba que debía obtener mucho de las ecuaciones diferenciales. Se centra en parte en los solitones, pero otro pasaje de Einstien habla de que posiblemente «en las complejidades de las soluciones de las ecuaciones diferenciales no lineales debe haber margen para interpretaciones probabilísticas» La frase no es exactamente así y, cuando la leí no reflexioné demasiado sobre ella. Obviamente, a ojos modernos, éso me sonaba a la teoría del caos determinista, pero el caso es que en la época de Einstein aún no existía esa teoría, aunque posiblemente el problema de los tres cuerpos y los resultados de Poincaré al respecto, que contenían el germen de la teoría del caos, sí eran conocidos por Einstein, pero no explicaré por ahora nada más al respecto. Diré, éso sí, que quizás el programa de Einstein podría reformularse de una manera mas clara en términos de dualidades, aunque, éso sí, no creo que ni aún así pudiera realizarse, aunque es divertido pensar en como podría intentar hacerse.

Planeo hacer otra entrada, en parte continuación de ésta, dónde me extenderé sobre las teorías de unificación. Realmente leyendo he descubierto cosas muy sorprendentes porque, por ejemplo, hubo gente (Weyl y Klein) que intentó obtener una ecuación, que debería ser lo que luego fué la ecuación de Schröedinger, pero inspirados en una quinta dimensión, y las ideas de Kaluza, y de los propios Weyl y Klein, en las que también trabajó Einstein. Aparte de éso también planeo hablar más sobre la relación de Einstein con la cuántica, pero usando conceptos relacionados con esas teorías de unificación. A ver sí no tardo mucho en tenerla lista 😉

Genius, una serie sobre Einstein

Hace muy poco national geographic ha emitido una serie sobre la figura de Einstein titulada genious.

Einstein de joven.

La serie está muy bien desde diversos puntos de vista y, la verdad, hacía falta porque, hasta dónde recuerdo, hacía ya mucho tiempo que no había una serie o película sobre la figura de Einstein. La última, y de hecho la única, que recuerdo la ví antes de empezar la carrera de físicas, así que no pude apreciar ni una pequeña fracción de los detalles que he podido apreciar en ésta y así he podido resolver algunas dudas que me habían ido surgiendo.

Una duda, que imagino mucha gente que haya estudiado físicas y conozca por encima la vida de Einstein tendrá, es todo el asunto de la oficina de patentes. Es bien sabido que el pobre Einstein no pudo obtener, por desavenencias con un destacado profesor de la universidad dónde estudió, una plaza para hacer un doctorado tras terminar sus estudios de grado, y que tuvo que trabajar en una oficina de patentes. De manera muy sorprendente mientras estaba en esa oficina logró publicar una serie de artículos revolucionarios, incluyendo el de la teoría especial de la relatividad.

Se ha intentando vender la idea, mitad «romántica» mitad «motivacional» de que sí alguien es realmente bueno va a poder conseguir el éxito independientemente de las adversidades, pero éso, sencillamente, no se corresponde con la realidad. Además, esa superchería neoliberal está orientada hacia los emperderores (emprendedores) que intentan crear una pequeña empresa desde el «garaje» y a partir de ahí hacerse poco a poco millonario, lo cuál es algo que ocasionalmente funciona (microsoft, apple, las empresas de Elon Musk) pero en la mayoría de los casos no. Y, en particular, es sencillamente inviable en investigación porque, porque ¡no puedes montar una starup de investigación fundamental!.

Entonces ¿cómo es que Einstein logró esos logros en esa circunstancia? Es más, para complicar aún mas el asunto resulta que en ese momento acababa de tener un hijo, que ya se sabe que quitan un montón de tiempo. Éso podría llevar a pensar que, en realidad, buena parte de esas teorías las podría haber hecho la esposa de Einstein, física cómo él, y, dada la época, seguramente bastante inteligente porque difícilmente habría logrado apoyo de su familia y el éxito en los estudios sólo por que tuviera vocación. El caso es que el hijo era de ambos, y Einstein tenía que trabajar así que tampoco iba a tener mucho tiempo ¿no?

Bien, todo está mas o menos relacionado. Para empezar en la serie muestran, y es muy creíble, que Einstein no buscó un empleo regular nada más acabar los estudios. Tenía dinero de su familia y podía hacer trabajos ocasionales dando clases (de ese modo conoció a la gente del club Olimpia, que tendrían una cierta influencia en su vida intelectual de ese momento). Su idea era seguir así hasta encontrar una plaza en alguna universidad, pero tuvo el problema de que Mileva se quedó embarazada y se vió obligado a buscar un trabajo a jornada completa. En la serie reflejan muy bien la repulsa y desesperación que esa decisión suponía para él, cómo lo sería para cualquier físico auténtico que se viera en similar circunstancia. El caso es que aunque el primer hijo de Mileva falleció tuvieron un segundo (la gente no aprecia realmente lo que han cambiado la sociedad las medidas profilácticas, y lo que aún la va a seguir cambiando). Afortunadamente para ellos la familia de Mileva siempre había apoyado el deseo de su hija de ser científica y la madre se desplazó al domicilio de la familia para ocuparse del bebé y así dejar tiempo a que Mileva pudiera dedicarse a investigar, aunque no estuviera en una plaza universitaria, que también era su deseo, no sólo Einstein tuvo que sufrir por no poder investigar. Por cierto, hay estudios que demuestran que las hembras de mucho mamíferos ven aumentada su capacidad intelectual, en algunos campos, al tener hijos, y todo apunta a que podría pasar algo similar en las hembras humanas,lo cuál le habría venido bien a Mileva.

Mileva Maric, con Einstien al fondo.

Entonces parece que todo apuntaría a que Mileva podría ser la verdadera creadora de la relatividad especial y el resto de trabajos de 1905, el año mirábilils. Pero, por otro lado, hay mucha evidencia documentada de que Einstein había meditado durante bastante tiempo sobre las ideas que surgieron ese año, así que, en todo caso, Mileva no podría nunca tener todo el mérito. Pero, sí Esintein no podía investigar por falta de tiempo ¿entonces qué?. Ahí es dónde la serie da respuestas. Para empezar Einstein obtuvo ese puesto vía recomendaciones y tenía una ligera manga ancha (pero no demasiado) para intentar hacer algo en la oficina sin que le despidieran, aunque, la verdad, muy poco. Tenía que dedicar las noches y fines de semana, y, aún así, no le bastaba. Tras haber, pese a todo, logrado publicar un primer artículo, pidió ayuda a quien le había conseguido el puesto y logró que un compañero y amigo de la carrera entrara a trabajar en la oficina (algo que le venía bien ya que también se había casado) y le ayudase con su trabajo en la oficina de patentes, dándole así mas tiempo a trabajar en sus ideas dentro de la propia oficina. Aparte, siendo bueno en matemáticas, ése amigo también le ayudaba con los cálculos.

Pese a todo en la serie muestran cómo Einstein pide ayuda a Mileva a que le ayude a demostrar los detalles matemáticos de algunas de las ideas, cuando ya tenía del todo clara la solución a nivel conceptual. Mas adelante muestran cómo Mileva le reprocha que Einstein mencionara en un artículo la ayuda de su amigo, pero no dijera nada de ella. Albert aducía que se daba por sobreentendio que tenían un proyecto común y que, por supuesto, valoraba mucho su contribución, pero, la verdad, tal cuál se muestra queda fatal. Para contrastar en la serie muestran el caso del matrimonio Curie, dónde Pierre rechaza el premio nobel sino incluyen en el mismo a su esposa. Aparte de por el contraste la presencia de los Curie es relevante científicamente, pués la prueba del famoso E=mc^2 fue ilustrada por primera vez por el decaimiento radiactivo que descubrieron los Curie, y por la posterior relación de Marie Curie con la familia Einstein.

En cualquier caso eran cálculos bastante sencillos casi todos los que estaban involucrados en las teorías de esa época y una investigación mas exigente, cómo la de la relatividad general, hubiera sido absolutamente inviable en semejantes condiciones.

Otro aspecto que tratan muy bien es el tema de la ciencia Alemana en ese momento. Ahí juega un papel importante Lienard (creo que es el del potencial de lienard en electromagnetismo, pero no estoy seguro) que terminaría siendo un científico al servicio del nazismo y que defendía una ciencia muy limitada de miras, totalmente opuesta a la de Einstein. Einstein nunca se sintió Alemán y, de hecho, estudió la carrera en Suiza, mucho mas liberal (en sentido social e intelectual) que Alemania. En la serie muestran cómo muchos de los grandes científicos huyeron de Alemania en los albores del gobierno de Hitler, bien porque eran judios y les echaban de sus plazas, bien porque no simpatizaban con el gobierno nazi. Para ampliar lo que se ve en la serie hice una búsqueda y encontré el siguiente artículo Historias de matemáticas: Nazis y matemáticas. Crónica de una barbarie

Lienard, y otros científicos nazis, no sólo tenían una visión de la ciencia limitada sino que decían que esa visión era la «ciencia alemana» y que se oponía, en particular a la ciencia judia. Por absurdo que parezca esa gente revindicaba una «pureza» de la ciencia alemana, que, tal cómo la plantean, viene a decir que los alemanes puros de raza aria son gente cuadriculada «sin imaginación, sólo una intuición elemental», y sin ninguna capacidad intelectual de abstracción digna de mención, lo cuál es muy grave en ramas cómo la física y las matemáticas. También, curiosamente, protestan contra el rigor, con lo cual , básicamente, lo que piden es eliminar cualquier aspecto de la matemática que la haga difícil y útil. Además, sólo están interesados en ciencia con aplicación inmediata, lo cuál, por supuesto, es firmar la sentencia de muerte para la ciencia fundamental,y, al poco tiempo, de la propia ciencia aplicada.

Pese a que en la época del ascenso de Hitler al poder absolutamente ningún físico de primera línea, dentro o fuera de Alemania. tenía la menor duda sobre la valía del trabajo de Einstein, los segundones aprovecharon para conseguir un reconocimiento que no se correspondía en absoluto con sus nulos méritos, y de hecho nadie les recuerda o estudia ahora.

El caso es que, sí uno va a plantearse quien es quien en matemática alemana tenemos a Carl Friederich Gauss y a Riemman cómo los nombres mas destacados, y, aunque no le he podido corroborar en una rápida búsqueda, me parece que son judios, pero había muchos más.

Dije antes que se habían ido la mayoría de grandes científicos, y el artículo que enlace da muchos detalles que lo ilustran. En particular es esclarecedor la lista de matemáticos que tuvieron que salir por piernas del régimen nazi, bien, cómo decía antes, porque les echaban de la universidad por una ley, bien porque fueron lo bastante listos para entender que si se quedaban los iban a terminar matando. Sí uno mira la lista, y sabe del tema, reconocerá un montón de nombres muy famosos a nivel mundial, encabezados por gente como Jonh Von Neuman, Kurt Goedel, Herman Weyl, Emmy Nöether, Felix Hausdorf, Rudolf Carnap, Robert Openheimer, Paul Hertz, Richard Courant, etc (un etcétera en el que dejo fuera a gente muy de primera fila, tanto cómo los anteriores) algunos famosos también por sus contribuciones a la física. Al final del artículo vienen algunas notas sobre los logros y obras de varios de ellos.

Por supuesto en la física pasó lo mismo y, aparte de Einstein, huyó de allí casi toda la élite de la física Germana (osea, con la excepción de Heissenberg todos) mucha de ella judia, o con ascendencia judia, o simplemente disconforme con el régimen nazi.

Es decir, que antes de empezar la guerra los nazis habían expulsado a toda su élite científica. En fin, recomiendo leer el artículo, porque el nivel de majaderías de los matemáticos nazis está casi a la altura de los postmodernistas franceses. Digo casi porqué, admitámoslo, ésos eran aún mas estúpidos, pero bueno, al menos eran filósofos y no científicos y la vergüenza no recae sobre la ciencia 😛

En la parte del rigor científico y la claridad de la explicación pedagógica de las ideas la serie hace un trabajo excelente. Según tengo entendido el encargado de la parte científica es el físico de cuerdas Clifford Jonsohn, famoso en el campo por haber publicado el libro de texto D-branes, cuya lectura recomiendo, por cierto, aunque en algunos pasajes se complica, en mi opinión, demasiado.

He seleccionado esos dos tópicos, pero hay muchos más, y he comentado sobre ellos la parte que mas me ha interesado, y no necesariamente con el enfoque que hacen en la serie. Recomiendo sin falta verla, son 10 episodios, tanto por la importancia de la figura de Einstein, cómo por la descripción del ambiente académico y social de la época. Señalo ya que, aparte de Einstein, aparecen por la serie muchos de los grandes físicos y matemáticos relevantes a la historia de un modo u otro.

Motivado por la serie me leí un libro sobre las teorías de unificación de Einstein al cuál dedicaré en el futuro (espero que cercano) una entrada propia.

¿Es la fenomenología de cuerdas un oxymoron?

En esta entrada me voy a referir principalmente a un artículo, del mismo título, Is String Phenomenology an Oxymoron? de Fernando Quevedo. El artículo es un ensayo que esta relacionado con una charla que dió en la conferenecia  Why truust a theory?  en Michin, en Diciembre de 2015.

El índice del artículo es el siguiente:

Contents 1

Introduction 1

2 Basic Theories 4

3 General predictions of Quantum Field Theories 5

4 The Standard Model and Beyond 6

5 General predictions of String Theory 11 6 Four-dimensional Strings 15

6.1 Model Independent Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

6.2 The Landscape . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

6.2.1 Supersymmetry Breaking . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

6.2.2 Models of Inflation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

7 Criticisms to String Phenomenology 23

8 Final Remarks 27

A A timeline of developments in string phenomenology 30

B Ten open questions for BSM 32

C Some open challenges for string phenomenology 32

Cómo se puede ver el artículo cubre muchos tópicos en muy pocas páginas, así que sí no se tiene una cierta idea sobre lo que se está hablando es difícil que se entienda algo. Pero sí se tiene una base resulta muy didáctico, aporta bastantes detalles interesantes y muestra la relación entre varios tópicos que son relativamente especializados.

Un ejemplo,  las compactificaciones tipo large, a las que el autor ha contribuido bastante, son una versión para valores altos de la constante de acoplo de los escenarios de KKLT para fijar los valores de los moduli.

También es interesante la información que da sobre el papel de los moduli en cosmología, de dónde, aparentemente, se puede extraer con una cierta firmeza que la masa de los mismos, que estará ligada a la masa de las partículas supersimétricas mas ligeras, debería ser mayor que 30  TeV,  para no arruinar la bariogénesis. Éso supondría que quedarían fuera del alcance del LHC.

 

En la parte de conclusiones genéricas habla de que bastantes modelos, en particular KKLT y large,  favorecen lo que se conoce cómo «Split supersymmetry» dónde los fermiones compañeros supersimétricos de los bosones tendrían una masa mayor de 1 TeV mientras que los compañeros bosónicos de los fermiones (por ejemplo el stop, compañero del quark top) deberían tener una masa de entre 10 y 100 veces superior a la de las partículas supersimétricas fermiónicas, con lo cuál sí se hallase un stop o similar en el LHC quedarían descartadas esos escenarios.

No voy a intentar hacer un resumen de un artículo que ya es en si mismo un resumen. Simplemente recomiendo leerlo. Veo que ahora hay una versión 2 del mismo, y yo leí la versión 1, lo cuál me da la excusa perfecta para releerlo, que aunque es relativamente fácil de entender (presenta los resultados, no cómo se llega a ellos) hay mucha información y es fácil que esta se olvide, o se mezcle en la memoria cómo le de la gana.

Aviso que la visión que da está algo influenciada por sus propias líneas de investigación, pero éso es algo completamente normal, y aún así, sigue dando una visión muy amplia de muchos aspectos de la fenomenologia de cuerdas que, ¡No, no es un oxymoron! 😉

 

 

 

 

Una guía compacta a la compactificación

En su momento escribí una entrada sobre la forma mas básica de compactificación, la teoría de Kaluz-Klein. Sí se quieren mas detalles (en especial cómo aparece, y que papel juega el dilatón) de los que vienen en esa entrada se puede consultar, por ejemplo, la correspondiente entrada de la wikipedia inglesa Kaluza–Klein theory.

Bien, voy a intentar avanzar un poco más respecto a lo que ahí viene y dar una idea un poco global de cómo es el proceso de compactificación. Al intentar dar una idea global dejaré de lado bastantes detalles técnicos, pero tampoco va a ser a nivel de un libro de divulgación para legos sino mas bien en la línea de la entrada anterior.

El siguiente paso, una vez tenemos una teoría guague abeliana U(1), es intentar obtener una teoría no abeliana, para lo cuál vamos a necesitar mas de una dimensión adicional, usando la notación de la entrada anterior descomponemos la métrica en la forma:

Recordemos que M y N son índices que recorren todas las dimensiones, mu y nu recorren sólo las 4 dimensiones usuales, eta es la métrica de Minkowsky e y denota las coordenadas en las dimensiones extra.

Asumimos que esta métrica es una solución a las ecuaciones de Einstein para el vacío o bien, sí permitimos una contaste cosmológica

En el caso de una sóla dimensión adicional la compactificación era única, convertir el eje y en un círculo, ahora tenemos mucha mas libertad. Sí tenemos D dimensiones extra y plegamos cada uno de los ejes coordenados en un círculo tendremos un D-toro (recordemos que el 2-toro tiene forma de «donut» hueco, o de neumático) y, en ése caso, la gravedad de las dimensiones extra se verá cómo una teoría gauge . Mas adelante explicaré cómo se obtiene ese D-toro, pero de momento entendamos bien lo que hemos hecho. Cuando las dimensiones extra están descompactificadas ahí opera la simetría del grupo de difeormorfismos de esas dimensiones extra, que es muy grande. Al reducir esas dimensiones a la forma de un D-toro esa simetría de difeomorfismos se ha visto muy reducida, a ese . Digamos que el grupo de isommetrías de la dimensión compactificada se ve cómo una teoría gauge con esa misma simetría en las 4 dimensiones.

Cuando las dimensiones extra se compactifican a una geometría mas compleja que un D-toro y no es nada sencillo ver las isometrías de ese espacio. Voy a entrar un poco en algunos detalles matemáticos, elementales, pero que no siempre se comentan en los libros de física sobre el proceso de compactificación (sobre los detalles de las isomerías hablaré en otra entrada). Lo primero es el origen del término «compactificar». Hace referencia al concepto topológico de espacio compacto. Lo escribí en la entrada que dediqué a un libro sobre la conjetura de Poincaré pero lo reescribiré aquí, para hacer ésto mas autocontenido.

Las nociones de continuidad en cálculo se suelen dar en términos de epsilones y deltas, pero eso en esencia es hablar de entornos abiertos de la recta real, y el caso es que si uno lo analiza uno usa sólo 3 propiedades básicas de los abiertos.

Una topología es recoger esas tres propiedades y convertirlas en axiomas.

Sea X un conjunto y sea Y={Xn} una colección finita o infinita de subconjuntos de X, X e Y forman un espacio topológico si
i. el conjunto vacío e Y pertenecen a Y
ii. Cualquier subcolección finita o infinita {Zn} de Xn tiene la propiedad de que la unión de todos los Zn pertenece a Y
iii. Cualquier subcolección finita {Zm} de los Xn tiene la propiedad de que su intersección pertenece a Y.

Los Xn son los abiertos de esa topología. Conviene hacer una pequeña distinción, que no siempre se explica en los libros de topologia/geometría para físicos. Los intervalos epsilón y deltas del cálculo de una varible, y sus generalizaciones elmentales, los discos abiertos de radio epsilon/delta en el plano, las bolas abiertas en tres dimensiones, etc, son un tipo especial de abiertos, pero, ciertamente, hay conjuntos que son abiertos y no son de esa forma. Esos subconjuntos especiales de la topología forman una base de la misma.

Bien, una vez que tenemos definidos los abiertos cualquier definición que hagamos en términos de esos conjuntos va a ser una definición topológica. Por ejemplo se dice que un conjunto es cerrado cuando su complementario es abierto. Otra noción topologica de interés es la de compacidad. Intuitivamente en un compacto va a ser un conjunto cerrado y acotado (la distancia entre dos cualesquiera de sus puntos es finita).

Pero como dije una noción topológica debe darse en términos de los abiertos. Vamos a ello.

Primero debo explicar la idea de recubrimiento. Dado un subconjunto, S, de un espacio topológico, X un recubrimiento de S es una colección de conjuntos abiertos Rn tal que S esta incluido en la unión de todos los Rn. Se dirá que un conjunto es compacto cuando todo recubrimiento del mismo admite un subrecubrimiento (un cubrimiento con un un subconjunto de la colección recubridora)finito. La noción de compacidad es útil por muy diversos motivos. Una es que, por el teorema de Heine-Borel, podemos caracterizar los cerrados y acotados, un tipo de conjuntos interesante, mediante esta propiedad.Oto aspecto útil es que si queremos demostrar algo sobre un compacto nos basta demostrarlo sobre cualquier elemento del conjunto recubridor y asegurarnos de que la propiedad demostrada no se pierde cuando tenemos una unión finita de esos elementos. Es importante hacer notar que como en un compacto todos los recubrimientos admiten subrecubrimiento finito podemos elegir los Rn de la forma que mas nos convenga.

Tan importante es la noción de compacidad que la mayoría de resultados toopológicos van a estar referidos a espacios compactos. Los no compactos son mucho mas difíciles de estudiar.

Entonces la idea de la compactificación es coger un conjunto que no es compacto, por ejemplo la recta real, que no es acotada, y por tanto, según el teorema de Heine-Borel no es compacta, y convertirla en un conjunto compacto por un procedimiento bien definido, en este caso identificar los dos puntos del infinito a la «izquierda» y «derecha». Sí cogemos un folio e identificamos dos lados opuestos obtenemos la superficie de un cilindro (sin las tapas). Sí en ese cilindro resultante identificamos los dos círculos opuestos obtenemos un 2-toro.

ES interesante que, en el caso anterior, tanto el folio (un rectángulo con sus lados incluidos) cómo el toro son compactos así que aquí no estaría del todo justificado el término «compactificación». Pero sí nos imaginamos que el rectángulo es infinito, es decir, es el plano real, entonces sí estamos convirtiendo ese plano, que no es compacto, en un toro, que es compacto. Realmente el proceso de compactificación de un rectángulo aunque no cambia la compacidad del rectángulo si cambia otras propiedades topológicas del mismo, por ejemplo la conectividad por arcos (la explico en la entrada sobre la conjetura de Poincaré). El rectángulo es contractible (cualquier círculo que dibuje dentro del mismo se puede contraer a un punto sin salirse del rectángulo) mientras que en el toro no es así (de hecho hay dos familias de círculos que no pueden contreaerse a un punto). No daré mas detalles sobre ésto ahora (en el post sobre la conjetura de Poincaré comento más al respecto) pero no deja de ser un hecho interesante, que tiene muchas implicaciones en topología y en física.

Uno, bastante conocido, es que, en teoría de cuerdas, en particular para la cuerda heterótica compactificada en un Calabi-Yau, el número de generaciones de partículas es igual a la mitad de la característica de Euler-Poincaré de el espacio de compactificación M &latex\frac{1}{2}\chi (M))$. Esta constante apareció por primera vez en el trabajo sobre teoría grafos que hizo Euler para, entre otras cosas, resolver el problema de los puentes de Königsberg. Para un grafo la expresión de la característica de Euler es donde C, A y V son los números de caras, de aristas y de vértices respectivamente.

Cómo una superficie puede ser triangulada se puede definir esa constante en términos de la constante de Euler de la triangulación de la misma. No obstante, para una superficie, o una variedad n-dimensional, es mejor definir la constante en términos de los grupos de homología o cohomología. Primero se define el n-ésimo número de Betti &latex b_n$ cómo el rango del n-ésimo grupo de homología. En términos de esos números la característica de ÇEuler es la suma alternada de los números de Betti, es decir, tiene la expresión . También, mediante la dualidad de Poincaré, se podría escribir en términos de grupos de cohomología, así cómo en otras formas mas sofisticadas, pero éso ya sería irnos demasiado del propósito de la entrada.

Otro ejemplo es el uso de «Wilson loops» (o Wilson lines), osea, holonomías sobre círculos, que cuando el espacio no es conexo por arcos pueden usarse para reducir la simetría de un grupo gauge de una manera diferente al mecanismo de Higgs. Este procedimiento se usa de manera habitual en la fenomenología de la cuerda heterótica.

Por cierto, el plano real puede ser compactificado de manera natural de más de una forma. Un proceso muy típico sería la compactificación por un punto, el punto del infinito, es decir, cogemos todos las regiones del plano que «están en el infinito» y las convertimos en un punto. El espacio resultante sería una esfera. Es un proceso algo mas complejo de visualizar, y para ayudar a entenderlo vendría bien que explicase la proyección estereográfica, pero espero que con esta imagen os hagáis una idea aproximada.

Al inicio de la entrada mencioné que iba a explicar cómo surgía el D-toro al compactificar cada una de las dimensiones extra a un círculo. Hasta ahora he explicado cómo obtener el toro identificando los lados opuestos de un cuadrado, pero ahí no se ve cómo surge a partir de círculos.

Bien, éso requiere el concepto de producto cartesiano de dos espacios topológicos. Sí tenemos dos espacios topológicos X1 y X2 su producto cartesiano es el conjunto X1xX2={x1,x2}, es decir, el conjunto de pares dónde el primer par, x1, es un elemento de el conjunto X1 y el segundo, x2, es un elemento del conjunto X». A partir de una base de las topología de X1 y X2 se puede formar una base de la topologia producto tomando el conjunto de todos los pares ordenados posibles formados con los elementos base. En caso de que no se haya entendido muy bien este párrafo tampoco pasa nada, que es bastante fácil de visualizar la explicación que daré ahora.

Si tenemos dos círculos y , el toro es el producto cartesiano de esos dos círculos . Intuitivamente podemos pensar que cogemos uno de los círculos y cada uno de los puntos de ese círculo lo hacemos girar 360 grados alrededor de otro círculo perpendicular. Se puede visualizar en el siguiente dibujo bastante bien la idea.

Obviamente un D-toro es la generalización de esa idea, osea, un producto cartesiano de D círculos, cada uno de los cuales se obtiene al compactificar cada uno de los ejes coordenados.

Una definición mas precisa de la topología de identificación requeriría una entrada de un blog por si misma, pero al menos espero que con ésto quede mas claro el origen del término y los ejemplos den una idea de cómo se visualiza.